题目内容
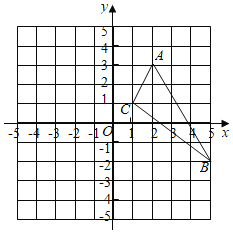
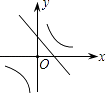
【题目】如图,一次函数![]() =
=![]() 的图像与正比例函数
的图像与正比例函数![]() =
=![]() 的图像相交于点A(2,
的图像相交于点A(2,![]() ),与
),与![]() 轴相交于点B.
轴相交于点B.

(1)求![]() 、
、![]() 的值;
的值;
(2)在![]() 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
【答案】(1)a=1,b=2;(2)点C的坐标为(0,2)或(0,-2).
【解析】
(1)利用正比例函数图象上点的坐标特征可求出点A的坐标,根据点A的坐标,利用待定系数法即可求出b的值;
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,根据三角形的面积公式结合△AOC的面积等于△AOB的面积,即可得出点C的坐标.
解:(1)把点A(2,a)的坐标代入y=![]() x,解得a=1.
x,解得a=1.
把点A(2,1)的坐标代入y=-![]() x+b,解得b=2.
x+b,解得b=2.
(2)把y=0代入y=-![]() x+2,解得x=4.
x+2,解得x=4.
∴点B的坐标为(4,0).
∴OB=4.
∵S△AOC=S△AOB,
∴![]() ×2·OC=
×2·OC=![]() ×4×1.
×4×1.
∴OC=2.
∴点C的坐标为(0,2)或(0,-2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?