题目内容
【题目】等腰三角形一腰长为5,一边上的高为3,则底边长为 .
【答案】8或 ![]() 或3
或3 ![]()
【解析】解:如图所示:

当等腰三角形为锐角三角形,且CD为腰上的高时,
在Rt△ACD中,AC=5,CD=3,
根据勾股定理得:AD= ![]() =4,
=4,
∴BD=AB﹣AD=5﹣4=1,
在Rt△BDC中,CD=3,BD=1,
根据勾股定理得:BC= ![]() =
= ![]() ;
;
当等腰三角形为钝角三角形,且CD为腰上的高时,
在Rt△ACD中,AC=5,CD=3,
根据勾股定理得:AD= ![]() =4,
=4,
∴BD=AB+AD=5+4=9,
在Rt△BDC中,CD=3,BD=9,
根据勾股定理得:BC= ![]() =3
=3 ![]() ;
;
当AD为底边上的高时,如图所示:
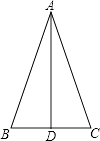
∵AB=AC,AD⊥BC,
∴BD=CD,
在Rt△ABD中,AD=3,AB=5,
根据勾股定理得:BD= ![]() =4,
=4,
∴BC=2BD=8,
综上,等腰三角形的底边长为8或 ![]() 或3
或3 ![]() .
.
所以答案是:8或 ![]() 或3
或3 ![]()
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?



