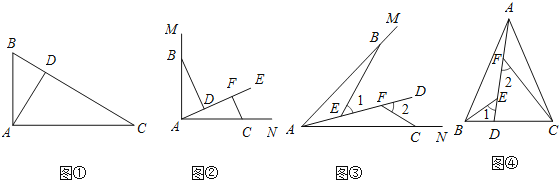
题目内容
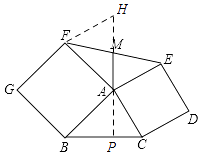
【题目】已知:如图,在△ABC中,cos∠ABC= ![]() ,sin∠ACB=
,sin∠ACB= ![]() ,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为 .
,AC=2,分别以AB,AC为边向△ABC形外作正方形ABGF和正方形ACDE,连接EF,点M是EF的中点,连接AM,则AM的长为 . 
【答案】![]()
【解析】解:如图,过F作AE的平行线,交AM的延长线于H,则∠HFM=∠AEM,∠H=∠EAM,
∵点M是EF的中点,
∴FM=EM,
∴△FHM≌△EAM,
∴AE=FH=AC,AM=MH= ![]() AH,
AH,
∵四边形ABCF是正方形,
∴AF=BA,
∵∠AFH+∠FAE=180°,∠CAB+∠HFA=180°,
∴∠AFH=∠BAC,
在△AFH和△BAC中,
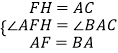 ,
,
∴△AFH≌△BAC(SAS),
∴AH=BC=2AM,
即AM= ![]() BC,
BC,
如图,过A作AP⊥BC于P,
∵cos∠ABC= ![]() ,sin∠ACB=
,sin∠ACB= ![]() ,AC=2,
,AC=2,
∴AP=AC×sin∠ACB=2× ![]() =
= ![]() ,CP=
,CP= ![]() AC=1,∠BAP=45°=∠ABP,
AC=1,∠BAP=45°=∠ABP,
∴BP=AP= ![]() ,
,
∴BC= ![]() +1,
+1,
∴AM= ![]() BC=
BC= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了正方形的性质和解直角三角形的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目