题目内容
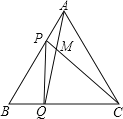
【题目】如图，利用热气球探测器测量大楼AB的高度．从热气球P处测得大楼顶部B的俯角为37°，大楼底部A的俯角为60°，此时热气球P离地面的高度为120m．试求大楼AB的高度（精确到0．1m）．（参考数据：sin37°≈0．60，cos37°≈0．80，tan37°≈0．75，
≈1．73）
【答案】大楼AB的高度约为68．1米．
【解析】
试题分析：首先过P作PC⊥AB，垂足为C，进而求出PC的长，利用tan37°=
，得BC的长，即可得出答案．
试题解析：过P作PC⊥AB，垂足为C，由已知∠APC=60°，∠BPC=37°，
且由题意可知：AC=120米．
在Rt△APC中，由tan∠APC=，
即tan60°=
，得PC=3
=40
．
在Rt△BPC中，由tan∠BPC=，
即tan37°=，得BC=40×0．75≈51．9．
因此AB=AC-BC=120-51．9=68．1，
即大楼AB的高度约为68．1米．
【题目】老张装修完新房，元旦期间到商场购买冰箱、电视机和洗衣机三件家电，刚好该商场推出新年优惠活动，具体优惠情况如下表：
购物金额（原价） | 折扣优惠 |
不超过3000元的部分 | 无折扣优惠 |
超过3000元但不超过10000元部分 | 九五折（ |
超过10000元的部分 | 九折 |
付款时，还可以享受单笔消费满2000元立减160元优惠 | |
如：买原价5000元的商品，实际花费：
（元）
（1）已知老张购买的这三件家电原价合计为11500元，如果一次性支付，请求出他的实际花费；
（2）如果在该商场购买一件原价为
元的商品（
）．请用含的代数式表示实际花费；
（3）付款前，老张突然想到：如果一次性支付，虽然折扣优惠更大，却只能享受一次立减160元优惠，如果将这三件家电分开支付或者两件合并支付．另一件单独支付，就可以享受多次立减160元优惠，已知老张购买的冰箱原价4800元，电视机原价4600元，洗衣机原价2100元，请你通过计算帮老张设计出最优惠的支付方案．
