题目内容
【题目】点C是直线l1上一点,在同一平面内,把一个等腰直角三角板ABC任意摆放,其中直角顶点C与点C重合,过点A作直线l2⊥l1,垂足为点M,过点B作l3⊥l1,垂足为点N

(1)当直线l2,l3位于点C的异侧时,如图1,线段BN,AM与MN之间的数量关系 (不必说明理由);
(2)当直线l2,l3位于点C的右侧时,如图2,判断线段BN,AM与MN之间的数量关系,并说明理由;
(3)当直线l2,l3位于点C的左侧时,如图3,请你补全图形,并直接写出线段BN,AM与MN之间的数量关系.
【答案】(1)MN=AM+BN;(2)MN=BN-AM,见解析;(3)见解析,MN=AM﹣BN.
【解析】
(1)利用AAS定理证明△NBC≌△MCA,根据全等三角形的性质、结合图形解答;
(2)根据直角三角形的性质得到∠CAM=∠BCN,证明△NBC≌△MCA,根据全等三角形的性质、结合图形解答;
(3)根据题意画出图形,仿照(2)的作法证明.
(1)MN=AM+BN
(2)MN=BN-AM
理由如下:如图2.
因为l2⊥l1,l3⊥l1
所以∠BNC=∠CMA=90°
所以∠ACM+∠CAM=90°
因为∠ACB=90°
所以∠ACM+∠BCN=90°
所以∠CAM=∠BCN
又因为CA=CB
所以△CBN≌△ACM(AAS)
所以BN=CM,NC=AM
所以MN=CM﹣CN=BN﹣AM
(3)补全图形,如图3
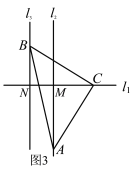
结论:MN=AM﹣BN
由(2)得,△CBN≌△ACM(AAS).
∴BN=CM,NC=AM
结论:MN=CN-CM=AM-BN.

【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.8千克时,t的值为( )
A. 128B. 132C. 136D. 140