Question

【题目】如图，已知CD⊥AB于点D，BE⊥ AC于点E， CD、 BE交于点O，且AO平分∠BAC，则图中的全等三角形共有_________________对。

Answer 1

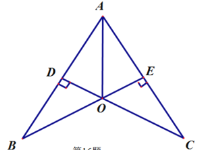
【答案】4

【解析】

先利用已知条件和隐含条件AO=AO确定△ADO≌△AEO，然后再利用由全等得到的条件，继续判定其他三角形的全等。

解：∵CD⊥AB，BE⊥AC，AO平分∠BAC

∴.∠ADO=∠AEO=90°，∠DAO=∠EAO AO=AO

∴△ADO≌△AEO；（AAS）

∴OD=OE，AD=AE

·∵∠DOB=∠EOC，∠ODB=∠OEC=90°

∴△BOD≌△COE：

∴.BD=CE，OB=OC，∠B=∠C

·∵AE=AD，∠DAC=∠CAB，∠ADC=∠AEB=90°

∴△ADC≌△AEB；（ASA）

∴AD=AE，BD=CE

又∵.AB=AC OB=OC，AO=A0

△ABO≌△ACO.（SSS）

故答案为4..