题目内容
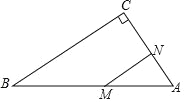
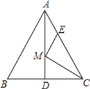
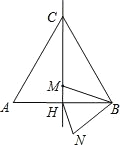
【题目】如图,在边长为 2a 的等边△ABC 中,M 是高 CH 所在直线上的一个动点, 连接 BM,将线段 BM 绕点 B 逆时针旋转 60°得到 BN,连接 HN,则在点 M 运动的过程中,线段 BN 长度的最小值为___________ .
【答案】a.
【解析】
首先取BC的中点D, 又已知条件可证得△HBN≌△DBM , 在点M运动的过程中, 要使线段BN的长度最小,即M点与H点重合,可得BN 长度的最小值.
解:如下图所示, 
如图, 取BC的中点D, 连接MD.
![]() △ABC 为等边三角形, CH为AB边上的高,
△ABC 为等边三角形, CH为AB边上的高,
![]() AB=BC,∠ABC=60
AB=BC,∠ABC=60![]() ,H为AB的中点.
,H为AB的中点.
![]() D为BC的中点,
D为BC的中点,![]() BD=BH.
BD=BH.
由旋转知, ∠MBN=60![]() , BM=BN,
, BM=BN,
![]() ∠DBM=∠HBN,
∠DBM=∠HBN,
![]() △HBN≌△DBM(SAS),
△HBN≌△DBM(SAS),
![]() BN=BM.
BN=BM.
在点M运动的过程中, 要使线段BN的长度最小,即M点与H点重合,此时BN=BM=BH=a,
故BN的最小值为a.
故答案:a.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目