题目内容
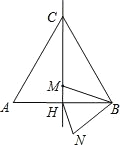
【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
在AB上取AE′=AE,连接CE′,过点E′作E′F⊥BC由等边三角形的性质可知:AB=AC=BC=6,∠B=60°,然后证明△AE′M≌△AEM,从而得到E′M=EM,由两点之间线段最短可知:当E′、M、C在一条直线上时,EM+MC有最小值,在Rt△E′BF中,可求得BF=2,E′F=![]() ,最后在Rt△E′FC中,由勾股定理求E′C的长即可.
,最后在Rt△E′FC中,由勾股定理求E′C的长即可.
解:如图所示,在AB上取AE′=AE,连接CE′,过点E′作E′F⊥BC.
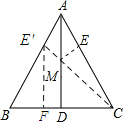
∵△ABC为等边三角形,
∴AB=AC=BC=6.
∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD.
在△AE′M和△AEM中,
 ,
,
∴△AE′M≌△AEM,
∴E′M=EM.
由两点之间线段最短可知:当E′、M、C在一条直线上时,EM+MC有最小值.
∵AE=2, ∴BE′=AB-AE′=4
在Rt△E′BF中,∠B=60°,
∴ ![]() ,
,![]() .
.
∴BF=![]() BE′=
BE′=![]() ×4=2,E′F=
×4=2,E′F= ![]() BE′=
BE′=![]() ×4=
×4=![]() .
.
∴FC=BC-BF=4.
在Rt△E′FC中,
E′C![]() .
.
∴EM+MC=![]() .
.
故选:C.

练习册系列答案
相关题目