题目内容
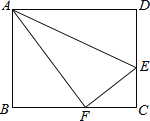
【题目】如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
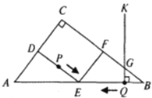
(1)D,F两点间的距离是 ;
(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值.若不能,说明理由;
(3)当点P运动到折线EF-FC上,且点P又恰好落在射线QK上时,求t的值;
(4)连结PG,当PG∥AB时,请直接写出t的值.
【答案】(1)25;(2)能,t=![]() ;(3)
;(3)![]() ,
,![]() ;(4)
;(4)![]() 和
和![]()
【解析】
(1)根据中位线的性质求解即可;
(2)能,连结![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,由四边形
,由四边形![]() 为矩形,可知
为矩形,可知![]() 过
过![]() 的中点
的中点![]() 时,
时,![]() 把矩形
把矩形![]() 分为面积相等的两部分,此时
分为面积相等的两部分,此时![]() ,通过证明
,通过证明![]() ,可得
,可得![]() ,再根据
,再根据![]() 即求出t的值;
即求出t的值;
(3)分两种情况:①当点![]() 在
在![]() 上
上![]() 时;②当点
时;②当点![]() 在
在![]() 上
上![]() 时,根据相似的性质、线段的和差关系列出方程求解即可;
时,根据相似的性质、线段的和差关系列出方程求解即可;
(4)(注:判断![]() 可分为以下几种情形:当
可分为以下几种情形:当![]() 时,点
时,点![]() 下行,点
下行,点![]() 上行,可知其中存在
上行,可知其中存在![]() 的时刻;此后,点
的时刻;此后,点![]() 继续上行到点
继续上行到点![]() 时,
时,![]() ,而点
,而点![]() 却在下行到点
却在下行到点![]() 再沿
再沿![]() 上行,发现点
上行,发现点![]() 在
在![]() 上运动时不存在
上运动时不存在![]() ;当
;当![]() 时,点
时,点![]() ,
,![]() 均在
均在![]() 上,也不存在
上,也不存在![]() ;由于点
;由于点![]() 比点
比点![]() 先到达点
先到达点![]() 并继续沿
并继续沿![]() 下行,所以在
下行,所以在![]() 中存在
中存在![]() 的时刻;当
的时刻;当![]() 时,点
时,点![]() ,
,![]() 均在
均在![]() 上,不存在
上,不存在![]() .
.
解:(1)∵D, F分别是AC, BC的中点
∴DF是△ABC的中位线
∴![]()
(2)能.
连结![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
由四边形![]() 为矩形,可知
为矩形,可知![]() 过
过![]() 的中点
的中点![]() 时,
时,
![]() 把矩形
把矩形![]() 分为面积相等的两部分.
分为面积相等的两部分.
(注:可利用全等三角形借助割补法或用中心对称等方法说明),
此时![]() .
.
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵F是BC的中点
∴![]()
∴![]() .
.
故![]() .
.

(3)①当点![]() 在
在![]() 上
上![]() 时,如图1.
时,如图1.
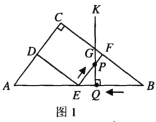
![]() ,
,![]() ,
,
由![]() ,得
,得![]() .
.
∴![]() .
.
②当点![]() 在
在![]() 上
上![]() 时,如图2.
时,如图2.
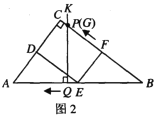
已知![]() ,从而
,从而![]() ,
,
由![]() ,
,![]() ,得
,得![]() .
.
解得![]() .
.
(4)![]() 和
和![]() .
.
(注:判断![]() 可分为以下几种情形:当
可分为以下几种情形:当![]() 时,点
时,点![]() 下行,点
下行,点![]() 上行,可知其中存在
上行,可知其中存在![]() 的时刻;此后,点
的时刻;此后,点![]() 继续上行到点
继续上行到点![]() 时,
时,![]() ,而点
,而点![]() 却在下行到点
却在下行到点![]() 再沿
再沿![]() 上行,发现点
上行,发现点![]() 在
在![]() 上运动时不存在
上运动时不存在![]() ;当
;当![]() 时,点
时,点![]() ,
,![]() 均在
均在![]() 上,也不存在
上,也不存在![]() ;由于点
;由于点![]() 比点
比点![]() 先到达点
先到达点![]() 并继续沿
并继续沿![]() 下行,所以在
下行,所以在![]() 中存在
中存在![]() 的时刻;当
的时刻;当![]() 时,点
时,点![]() ,
,![]() 均在
均在![]() 上,不存在
上,不存在![]() .)
.)

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案