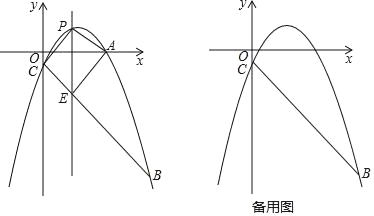
题目内容
【题目】如图，已知抛物线y=﹣
x2+bx+c经过点A（5，
）、点B（9，﹣10），与y轴交于点C，点P是直线AC上方抛物线上的一个动点；
（1）求抛物线对应的函数解析式；
（2）过点P且与y轴平行的直线l与直线BC交于点E，当四边形AECP的面积最大时，求点P的坐标；
（3）当∠PCB=90°时，作∠PCB的角平分线，交抛物线于点F．
①求点P和点F的坐标；
②在直线CF上是否存在点Q，使得以F、P、Q为顶点的三角形与△BCF相似，若存在，求出点Q的坐标；若不存在，请说明理由．
【答案】（1）y=﹣
x2+2x﹣1；（2）点P坐标为（
，
）；（3）①P（3，2），F（6，﹣1）;②存在，理由见解析，点Q的坐标为（4，﹣1）或（﹣3，﹣1）
【解析】
（1）根据抛物线
经过点A
，点B
，运用待定系数法即可求得抛物线对应的函数表达式；
（2）根据直线BC为：
可设点P的坐标为
则E
进而得到PE=
最后根据四边形AECP的面积=△APE面积+△CPE面积，求得点P坐标为
（3）①根据∠PCB=90°，CF平分∠PCB，可得∠BCF=45°，进而得出CF∥x轴，则当y=-1时，
解得F
再根据直线CP为：
可得当
时，可得P
②根据直线CB： 直线PF：
可得CB∥PF，即可得到∠BCF=∠PFC=45°，故在直线CF上存在满足条件的点Q，再设Q
由题可得CF=6，CB=
PF=
最后分两种情况进行讨论：当△PFQ1∽△BCF时，当△PFQ∽△FCB时，分别求得t的值，即可得出点Q的坐标为
（1）∵抛物线y=﹣
x2+bx+c经过点A（5， 
）、点B（9，﹣10），
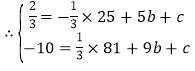
解得
∴抛物线对应的函数表达式为
（2）由抛物线可得，C（0，﹣1），B（9，﹣10），
∴直线BC为：y=﹣x﹣1，
设点P的坐标为（m，﹣m2+2m﹣1），则E（m，﹣m﹣1），
∴PE=﹣m2+2m﹣1﹣（﹣m﹣1）=﹣m2+3m，
∴四边形AECP的面积=△APE面积+△CPE面积
= 
×（﹣m2+3m）×m+×（﹣m2+3m）×（5﹣m）
=
（﹣m2+3m）
=﹣
m2+
m，
=﹣（m﹣）2+
，
∴当m=时，﹣m2+2m﹣1=，
∴点P坐标为
；
（3）①过点B作BH⊥
∵C（0，﹣1），B（9，﹣10），
∴CH=BH=9，
∴∠BCH=45°，
∵∠PCB=90°，CF平分∠PCB，
∴∠BCF=45°，
∴∠FCH=90°，即CF∥x轴，
当y=﹣1时，﹣1=﹣x2+2x﹣1，
解得x1=0，x2=6，
∴F（6，﹣1），
∵CP⊥CB，C（0，﹣1），
∴直线CP为：y=x﹣1，
当x﹣1=﹣x2+2x﹣1时，解得x1=0，x2=3，
当x=3时，y=2，
∴P（3，2）；
②∵直线CB：y=﹣x﹣1，直线PF：y=﹣x+5，
∴CB∥PF，
∴∠BCF=∠PFC=45°，
∴在直线CF上存在满足条件的点Q，
设Q（t，﹣1），
由题可得CF=6，CB=9
，PF=3，
（ⅰ）如图所示，当△PFQ1∽△BCF时，
，即
解得t=4，
∴Q1
（ⅱ）如图所示，当△PFQ∽△FCB时，
，即
解得t=﹣3，
∴Q2（﹣3，﹣1）．
综上所述，点Q的坐标为（4，﹣1）或（﹣3，﹣1）．
