题目内容
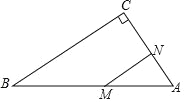
【题目】如图,在 Rt△ABC 中,∠C=90°,∠A=60°,AB=10cm,若点M 从点 B 出发以 2cm/s 的速度向点 A 运动,点 N 从点 A 出发以 1cm/s 的速度向点 C 运动,设 M、N 分别从点 B、A 同时出发,运动的时间为 ts.
(1)用含 t 的式子表示线段 AM、AN 的长;
(2)当 t 为何值时,△AMN 是以 MN 为底边的等腰三角形?
(3)当 t 为何值时,MN∥BC?并求出此时 CN 的长.
【答案】(1)AM=10﹣2t,AN=t;(2)t=![]() ;(3)当 t=
;(3)当 t=![]() 时,MN∥BC,CN=
时,MN∥BC,CN=![]() .
.
【解析】
(1)根据直角三角形的性质即可得到结论;
(2)根据等腰三角形的性质得到AM=AN,列方程即可得到结论.
(1)∵∠C=90°,∠A=60°,
∴∠B=30°,
∵AB=10cm,
∴AM=AB﹣BM=10﹣2t,AN=t;
(2)∵△AMN是以 MN为底的等腰三角形,
∴AM=AN,即10﹣2t=t,
∴当t=![]() 时,△AMN 是以MN为底边的等腰三角形;
时,△AMN 是以MN为底边的等腰三角形;
(3)当MN⊥AC时,MN∥BC,
∵∠C=90°,∠A=60°,
∴∠B=30°,
∵MN∥BC,
∴∠NMA=30°,
∴AN=![]() AM,
AM,
∴t=![]() (10﹣2t),解得t=
(10﹣2t),解得t=![]() ,
,
∴当t=![]() 时,MN∥BC,
时,MN∥BC,
CN=5﹣![]() ×1=
×1=![]() .
.

练习册系列答案
相关题目