题目内容
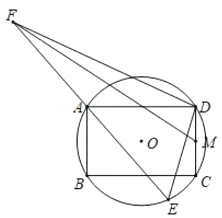
【题目】如图，⊙O的半径为
，四边形ABCD为⊙O的内接矩形，AD=6，M为DC中点，E为⊙O上的一个动点，连结DE，作DF⊥DE交射线EA于F，连结MF，则MF的最大值为_____．
【答案】
【解析】
如图，连接AC交BD于点O，以AD为边向上作等边△ADJ，连接JF，JA，JD，JM．判断出点F的运动轨迹，即可解决问题．
解：如图，连接AC交BD于点O，以AD为边向上作等边△ADJ，连接JF，JA，JD，JM．
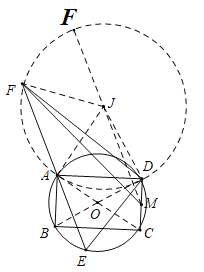
∵四边形ABCD是矩形，
∴∠ADC=90°，
∵AD=6，AC=
，
∴sin∠ACD=
，
∴∠ACD=60°，
∴∠FED=∠ACD=60°，
∵DF⊥DE，
∴∠EDF=90°，
∴∠EFD=30°，
∵△JAD是等边三角形，
∴∠AJD=60°，
∴∠AFD=
∠AJD，
∴点F的运动轨迹是以J为圆心JA为半径的圆，
∴当点F在MJ的延长线上时，FM的值最大，
此时FJ=6，JM=
，
则FM的最大值为；
故答案为：.
练习册系列答案
阅读快车系列答案
相关题目
