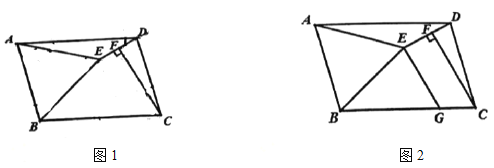题目内容
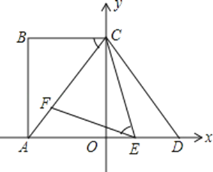
【题目】在△ABC中,AB=AC,∠BAC=90°,D为平面内的一点.
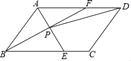
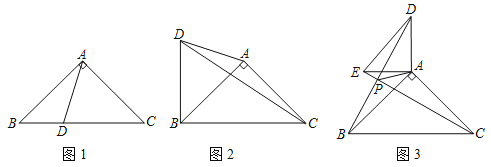
(1)如图1,当点D在边BC上时,且∠BAD=30°,求证:AD=![]() BD.
BD.
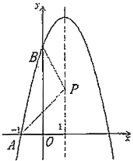
(2)如图2,当点D在△ABC的外部,且满足∠BDC﹣∠ADC=45°,求证:BD=![]() AD.
AD.
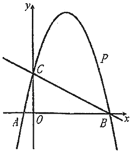
(3)如图3,若AB=4,当D、E分别为AB、AC的中点,把△DAE绕A点顺时针旋转,设旋转角为α(0<α≤180°),直线BD与CE的交点为P,连接PA,直接写出△PAC面积的最大值.
【答案】(1)见解析;(2)BD=![]() AD,见解析;(3)2+2
AD,见解析;(3)2+2![]()
【解析】
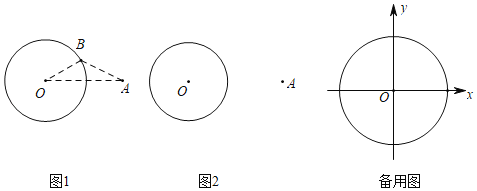
(1)如图1,将△ABD沿AB折叠,得到△ABE,连接DE,由折叠的性质可得AE=AD,BE=BD,∠EBD=∠ABD=45°,∠BAD=∠BAE=30°,可得∠DBE=90°,∠DAE=60°,由等腰直角三角形的性质和等边三角形的性质可得结论;
(2)如图2,过点A作AE⊥AD,且AE=AD,连接DE,由“SAS”可证△BAE≌△CAD,可得∠ACD=∠ABE,由“ASA”可证△DOB≌△DOE,可得DB=DE,由等腰直角三角形的性质可得结论;
(3)作PG⊥AC,交AC所在直线于点G,求出PG的最大值,即可求解.
(1)证明:如图1,将△ABD沿AB折叠,得到△ABE,连接DE,
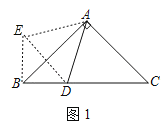
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵将△ABD沿AB折叠,得到△ABE,
∴△ABD≌△ABE,
∴AE=AD,BE=BD,∠EBD=∠ABD=45°,∠BAD=∠BAE=30°,
∴∠DBE=90°,∠DAE=60°,且AD=AE,BE=BD,
∴△ADE是等边三角形,DE=![]() BD,
BD,
∴AD=DE=![]() BD;
BD;
(2)证明:如图2,过点A作AE⊥AD,且AE=AD,连接DE,
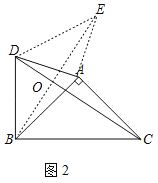
∵AE⊥AD,
∴∠DAE=∠BAC=90°,
∴∠BAE=∠DAC,且AD=AE,AB=AC,
∴△BAE≌△CAD(SAS)
∴∠ACD=∠ABE,
∵∠ACD+∠DCB+∠ABC=90°,
∴∠DCB+∠ABC+∠ABE=90°,
∴∠BOC=90°,
∵AE=AD,AE⊥AD,
∴DE=![]() AD,∠ADE=45°,
AD,∠ADE=45°,
∵∠BDC﹣∠ADC=45°,
∴∠BDC=∠ADC+45°=∠EDC,且DO=DO,∠DOB=∠DOE=90°,
∴△DOB≌△DOE(ASA)
∴BD=DE,
∴BD=![]() AD;
AD;
(3)如图3,作PG⊥AC,交AC所在直线于点G,
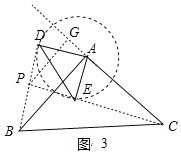
∵D,E在以A为圆心,AD为半径的圆上,
当CE所在直线与⊙A相切时,直线BD与CE的交点P到直线AC的距离最大,
此时四边形ADPE是正方形,AD=PD=2,
则CE=![]() =2
=2![]() ,
,
∴∠ACP=30°,
∴PC=2+2![]() ,
,
∴点P到AC所在直线的距离的最大值为:PG=1+![]() .
.
∴△PAC的面积最大值为![]() AC×PG=2+2
AC×PG=2+2![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案