题目内容
【题目】二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(1,0)、B(4,0).
(1)求此二次函数的表达式;
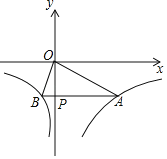
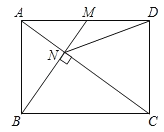
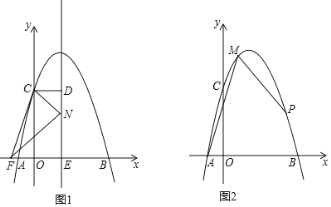
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(![]() ,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
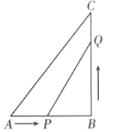
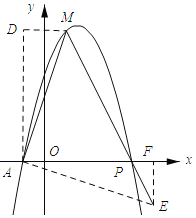
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标.
【答案】(1)![]() .
.
(2)N![]() 或N
或N![]() .
.
(3)P![]() .
.
【解析】
(1)直接把A(1,0)、B(4,0)坐标代入函数解析式求得![]() 的值,从而得到抛物线的解析式;
的值,从而得到抛物线的解析式;
(2)先求得抛物线的对称轴,然后求得CD,EF的长,设点N的坐标为(![]() )则ND=
)则ND=![]() ,NE=
,NE=![]() ,然后依据相似三角形的性质列出关于
,然后依据相似三角形的性质列出关于![]() 的方程,然后可求得
的方程,然后可求得![]() 的值;
的值;
(3)过点A作AD∥y轴,过点M作DM∥x轴,交点为D,过点A作AE⊥AM,取AE=AM,作EF⊥x轴,垂足为F,连结EM交抛物线与点P.则△AME为等腰直角三角形,然后再求得点M的坐标,从而可得到MD=2,AD=6,然后证明∴△ADM≌△AFE,于是可得到点E的坐标,然后求得EM的解析式为![]() ,最后求得直线EM与抛物线的交点坐标即可.
,最后求得直线EM与抛物线的交点坐标即可.
解:(1)把A(1,0)、B(4,0)代入y=ax2+bx+4
![]() 解得:
解得:![]()
所以二次函数为:![]() .
.
(2)因为CD⊥m,FE⊥m,
所以![]()
①当![]() 时,则
时,则 ![]()
因为抛物线的对称轴为![]() ,C(0,4)F(
,C(0,4)F(![]() ,0)
,0)
所以CD=![]() ,EF=
,EF=![]() ,设N(
,设N(![]() ,
,![]() )
)
所以NE=![]() ,DN=4-
,DN=4-![]() ,
,
所以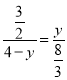 ,即
,即![]() ,
,
解得:![]() ,所以N(
,所以N(![]() ,2).
,2).
②当![]() 时,则
时,则![]() ,
,
所以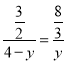 ,解得:
,解得:![]() ,
,
所以N(![]() ,
,![]() ),
),
综上可知N(![]() ,2)或N(
,2)或N(![]() ,
,![]() ).
).
(3) 如图所示:过点A作AD∥y轴,过点M作DM∥![]() 轴,交点为D,
轴,交点为D,
过点A作AE⊥AM,取AE=AM,作EF⊥![]() 轴,垂足为F,连结EM交抛物线与点P.
轴,垂足为F,连结EM交抛物线与点P.
∵AM=AE,∠MAE=90°,
∴∠AMP=45°.
将![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() ,
,
∴点M的坐标为(1,6). ∴MD=2,AD=6.
∵∠DAM+∠MAF=90°,∠MAF+∠FAE=90°,
∴∠DAM=∠FAE.
在△ADM和△AFE中

∴△ADM≌△AFE. ∴EF=DM=2,AF=AD=6.
∴E(5,-2).
设EM的解析式为![]() . 将点M和点E的坐标代入得:
. 将点M和点E的坐标代入得:
![]()
解得![]()
∴直线EM的解析式为![]() .
.
所以![]()
解得:![]() 或
或![]() , ∴点P的坐标为(4,0).
, ∴点P的坐标为(4,0).

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量P(百千克)与销售价格x(元/千克)满足函数关系式p=![]() x+8.从市场反馈的信息发现,该食材每天的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,部分数据如表:
x+8.从市场反馈的信息发现,该食材每天的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,部分数据如表:
销售价格x(元/千克) | 2 | 4 | …… | 10 |
市场需求量q(百千克) | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格x不低于2元/千克且不高于10元/千克,
(1)直接写出q与x的函数关系式,并注明自变量x的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种食材能全部售出;当每天的产量大于市场需求量时,只能售出市场需求的量,而剩余的食材由于保质期短作废弃处理;
①当每天的食材能全部售出时,求x的取值范围;
②求厂家每天获得的利润y(百元)与销售价格x的函数关系式;
(3)在(2)的条件下,当x为多少时,y有最大值,并求出最大利润.