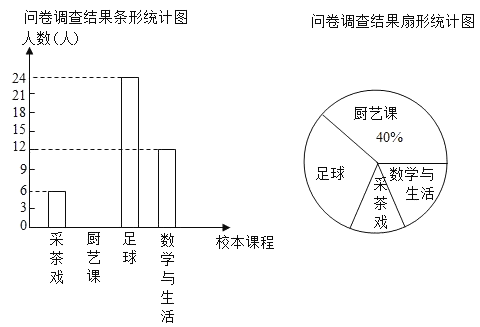
题目内容
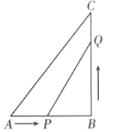
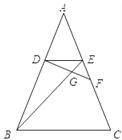
【题目】如图,△ABC,△EFG分别是边长为2和1的等边三角形,D是边BC,EF的中点,直线AG,FC相交于点M,当△EFG绕点D旋转一周时,点M经过的路径长为______.
【答案】![]()
【解析】
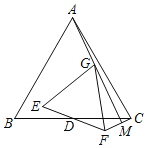
连接AD、DG,易证△ADG∽△CDF,∠DAG=∠DCF,通过推导角的关系证明∠AMC=90°,则点M在以AC为直径的圆周上运动,进而可解决问题.
如图,连接AD、DG.
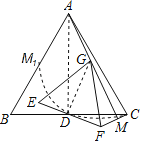
∵△ABC,△EFG均是边长为2和1的等边三角形,BD=CD,DE=DF,
∴AD⊥BC,GD⊥EF,
∴∠ADC=∠GDF=90°,
∴∠ADG=∠CDF,
∵![]() ,
,
∴△ADG∽△CDF,
∴∠DAG=∠DCF,
∵∠DAG+∠MAC+∠ACD=90°,
∴∠DCF+∠ACD+∠CAM=∠ACM+∠CAM=90°,
∴∠AMC=90°,
∴在旋转过程中,∠AMC=90°不变,
∴点M在以AC为直径圆周上运动,且点M运动的路径是来回共两个![]() 的圆周,
的圆周,
∴点M经过的路径长为![]() π,
π,
故答案为:![]() π.
π.

【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量P(百千克)与销售价格x(元/千克)满足函数关系式p=![]() x+8.从市场反馈的信息发现,该食材每天的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,部分数据如表:
x+8.从市场反馈的信息发现,该食材每天的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,部分数据如表:
销售价格x(元/千克) | 2 | 4 | …… | 10 |
市场需求量q(百千克) | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格x不低于2元/千克且不高于10元/千克,
(1)直接写出q与x的函数关系式,并注明自变量x的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种食材能全部售出;当每天的产量大于市场需求量时,只能售出市场需求的量,而剩余的食材由于保质期短作废弃处理;
①当每天的食材能全部售出时,求x的取值范围;
②求厂家每天获得的利润y(百元)与销售价格x的函数关系式;
(3)在(2)的条件下,当x为多少时,y有最大值,并求出最大利润.