题目内容
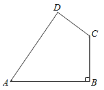
【题目】边长为a的正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
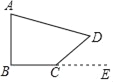
(1)若点F在边BC上(如图);
①求证:CE=EF;
②若BC=2BF,求DE的长.
(2)若点F在CB延长线上,BC=2BF,请直接写出DE的长.

【答案】(1)①证明见解析;②DE=![]() ;(2)DE=
;(2)DE=![]() .
.
【解析】
(1)①根据正方形的轴对称性可得△ABE≌△CBE,从而可得∠BAE=∠BCE,再根据∠ABC=∠AEF=90°,可得∠BAE=∠EFC,继而可得∠BCE=∠EFC,根据等角对等边即可得CE=EF;
②过点E作MN⊥BC,垂直为N,交AD于M,根据等腰三角形的性质结合已知条件可得![]() ,再根据四边形CDMN是矩形,△DME为等腰直角三角形,继而可求得ED的长;
,再根据四边形CDMN是矩形,△DME为等腰直角三角形,继而可求得ED的长;
(2)如图所示:过点E作MN⊥BC,垂直为N,交AD于M,由正方形的对称性可得△ABE≌△CBE,从而得∠BAE=∠BCE,继而由已知可得CE=EF,可得FN=CN,根据BC=2BF,可得FC=![]() a,继而可得EN=BN=
a,继而可得EN=BN=![]() a,由此即可求得DE=
a,由此即可求得DE=![]() a.
a.
(1)①∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF;
②过点E作MN⊥BC,垂直为N,交AD于M,
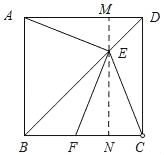
∵CE=EF,
∴N是CF的中点,
∵BC=2BF,
∴![]() ,
,
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED=![]() DM=
DM=![]() CN=
CN=![]() a;
a;
(2)如图所示:过点E作MN⊥BC,垂直为N,交AD于M,

∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=![]() a,
a,
∴CN=![]() a,
a,
∴EN=BN=![]() a,
a,
∴DE=![]() a.
a.

 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
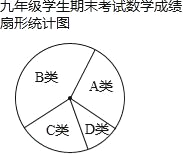
学练快车道口算心算速算天天练系列答案【题目】某学校为了解本校九年级学生期末考试数学成续情况,决定进行抽样分析,已知该校九年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有 .(只要填写序号)
①随机抽取一个班级的学生;②在全年级学生中随机抽取40名男学生:③在全年级10个班中各随机抽取4名学生.
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成分布统计图(不完整)如表格、图:①C、D类圆心角度数分别为 ;②估计全年级A、B类学生人数大约共有 .
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 0.3 | |
B类(60~79) | 0.4 | |
C类(40~59) | 8 | |
D类(0~39) | 4 |
(3)学校为了解其他学校数学成绩情况,将同层次的G学校和J学校的抽样数据进行对比,得下表:你认为哪所学校教学效果较好?说明你的理由.
学校 | 平均数(分) | 方差 | A、B类频率和 |
G学校 | 87 | 520 | 0.7 |
J学校 | 87 | 478 | 0.65 |