Question

【题目】如图，四边形ABCD中，∠ABC=Rt∠．已知∠A=α，外角∠DCE=β，BC=a，CD=b，则下列结论错误的是（　　）

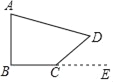
A. ∠ADC=90°﹣α+β B. 点D到BE的距离为bsinβ

C. AD= D. 点D到AB的距离为a+bcosβ

Answer 1

【答案】C

【解析】

如图所示，延长AD，BC交于点F，根据直角三角形两直角互余，可得∠F=90°﹣α，再根据∠ADC=∠F+∠DCE可判断A正确；如图所示，过D作DG⊥BC于G，利用三角函数可得DG=bsinβ，由此可判断B正确；如图所示，过D作DH⊥AB于H，则HD=BG= a+bcosβ，Rt△ADH中，利用三角函数可得AD=，由此可判断C错误；根据HD=BG=BC+CG=a+bcosβ，由此可判断D正确，

如图所示，延长AD，BC交于点F，

∵∠ABC=Rt∠，∠A=α，

∴∠F=90°﹣α，

∴∠ADC=∠F+∠DCE=90°﹣α+β，故A正确；

如图所示，过D作DG⊥BC于G，

∵∠DCE=β，CD=b，

∴DG=bsinβ，

即点D到BE的距离为bsinβ，故B正确；

如图所示，过D作DH⊥AB于H，则

HD=BG=BC+CG=a+bcosβ，

∴Rt△ADH中，AD=，故C错误；

∵HD=BG=BC+CG=a+bcosβ，

∴点D到AB的距离为a+bcosβ，故D正确，

故选C．