Question

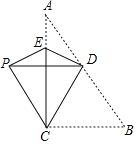
【题目】如图，菱形ABCD中，∠A是锐角，E为边AD上一点，△ABE沿着BE折叠，使点A的对应点F恰好落在边CD上，连接EF，BF．

（1）若∠A=70°，请直接写出∠ABF的度数．

（2）若点F是CD的中点，

①求sinA的值；

②求证：S△ABE=SABCD．

（3）设=k， =m，试用含k的代数式表示m．

Answer 1

【答案】（1）∠ABF =70°；（2）①sinA=；②证明见解析；（3）m= .

【解析】

（1）如图1中，由四边形ABCD是菱形，可得AB∥CD，∠C=∠A=70°，根据BA=BF=BC，可得∠BFC=∠C=70°，根据两直线平行，内错角相等即可求得∠ABF=∠BFC=70°；

（2）①如图2中，延长EF交BC的延长线于M，作BG⊥CD于G，由BC=BA=BF，继而可得cosA=cos∠BCG=，由此即可求得sinA=sin∠BCG=；

②由已知条件可得到△DEF≌△CMF，根据全等三角形的性质可得EF=FM，继而可推导得出S△ABE=SABCD；

（3）如图3中，设菱形的边长为a，先证明△MFC∽△MBF，可得FM2=MCMB，再根据AD∥MB，可得△DEF∽△CMF从而可得=m，由=k，可得DE=ka，AE=EF=（1﹣k）a，CM=，FM=，继而得[]2=（a+），可得出m=．

（1）如图1中，

∵四边形ABCD是菱形，

∴AB∥CD，∠C=∠A=70°，

∵BA=BF=BC，

∴∠BFC=∠C=70°，

∴∠ABF=∠BFC=70°；

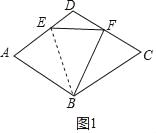
（2）①如图2中，延长EF交BC的延长线于M，作BG⊥CD于G．

∵BC=BA=BF，

∴CG=GF=CD=BC，

∴cosA=cos∠BCG=，

∴sinA=sin∠BCG=；

②∵四边形ABCD是菱形，F是CD中点，

∴DF=CF，∠D=∠FCM，∠EFD=∠MFC，

∴△DEF≌△CMF，

∴EF=FM，

∴S四边形BCDE=S△EMB，S△BEF=S△MBE，

∴S△ABE=SABCD；

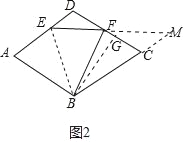
（3）如图3中，设菱形的边长为a．

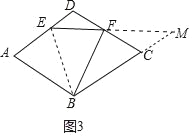
∵∠A=∠BFE=∠BCD，

∴∠MFC=∠DFE=∠FBC，∵∠M=∠M，

∴△MFC∽△MBF，

∴FM2=MCMB，

∵AD∥MB，

∴△DEF∽△CMF，

∴=m，

∵=k，

∴DE=ka，AE=EF=（1﹣k）a，CM=，FM=，

∴[]2=（a+），

∴m=．