题目内容
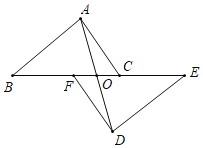
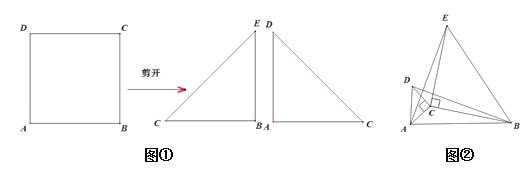
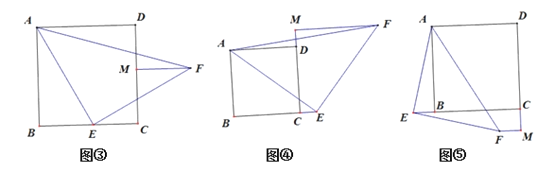
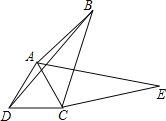
【题目】如图，在四边形ABCD中，∠ABC＝30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，若AB＝3，BC＝4，则BD＝（ ）
A.5B.5.5C.6D.7
【答案】A
【解析】
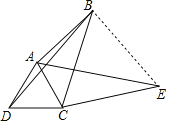
连接BE，如图，根据旋转的性质得∠BCE＝60°，CB＝CE，BD＝AE，再判断△BCE为等边三角形得到BE＝BC＝4，∠CBE＝60°，从而有∠ABE＝90°，然后利用勾股定理计算出AE即可．
解：连接BE，如图，
∵△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，
∴∠BCE＝60°，CB＝CE，BD＝AE，
∴△BCE为等边三角形，
∴BE＝BC＝4，∠CBE＝60°，
∵∠ABC＝30°，
∴∠ABE＝90°，
在Rt△ABE中，AE＝
＝5，
∴BD＝5．
故选：A．
孟建平错题本系列答案
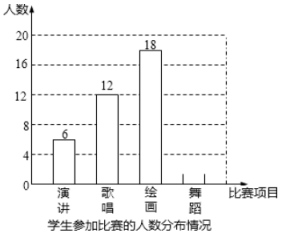
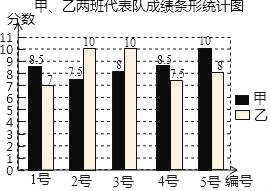
超能学典应用题题卡系列答案【题目】甲、乙两班分别选5名同学组成代表队参加学校组织的“国防知识”选拔赛，现根据成绩（满分10分）制作如图统计图和统计表（尚未完成）
甲、乙两班代表队成绩统计表
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | a | 0.7 |
乙班 | 8.5 | b | 10 | 1.6 |
请根据有关信息解决下列问题：
（1）填空：a＝ ，b＝ ；
（2）学校预估如果平均分能达8.5分，在参加市团体比赛中即可以获奖，现应选派 代表队参加市比赛；（填“甲”或“乙”）
（3）现将从成绩满分的3个学生中随机抽取2人参加市国防知识个人竞赛，请用树状图或列表法求出恰好抽到甲，乙班各一个学生的概率．
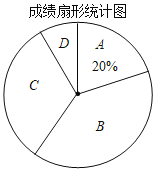
【题目】在第二届数字中国建设峰会召开之际，某校举行了第二届“掌握新技术，走进数时代”信息技术应用大赛，将该校八年级参加竞赛的学生成绩统计后，绘制成如下统计图表（不完整）：
成绩频数分布统计表
组别 | A | B | C | D |
成绩x（分） | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x＜100 |
人数 | 10 | m | 16 | 4 |
请观察上面的图表，解答下列问题：
（1）统计表中m＝ ，D组的圆心角为 °；
（2）D组的4名学生中，有2名男生和2名女生．从D组随机抽取2名学生参加5G体验活动，请你画出树状图或用列表法求：
①恰好1名男生和1名女生被抽取参加5G体验活动的概率；
②至少1名女生被抽取参加5G体验活动的概率．
