题目内容
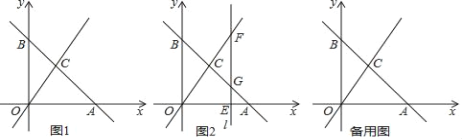
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm , 点P从点A出发,沿AB方向以每秒 ![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( ).
A.![]()
B.2
C.2 ![]()
D.3
【答案】B
【解析】连接PP′交BC于O ,
∵若四边形QPCP′为菱形,
∴PP′⊥QC ,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC ,
∴ ![]() ,
,
∵设点Q运动的时间为t秒,
∴AP= ![]() t , QB=t ,
t , QB=t ,
∴QC=6-t ,
∴CO=3- ![]() ,
,
∵AC=CB=6,∠ACB=90°,
∴AB= ![]() =6
=6 ![]() ,
,
∴ 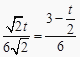 ,
,
解得:t=2,
故选:B.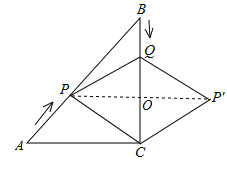
【考点精析】通过灵活运用勾股定理的概念和菱形的性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】已知甲、乙两种原料中均含有A元素,其含量及每吨原料的购买单价如下表所示:
A元素含量 | 单价(万元/吨) | |
甲原料 | 5% | 2.5 |
乙原料 | 8% | 6 |
已知用甲原料提取每千克A元素要排放废气1吨,用乙原料提取每千克A元素要排放废气0.5吨,若某厂要提取A元素20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.