题目内容
【题目】求证:相似三角形对应角的角平分线之比等于相似比.
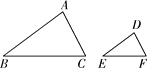
要求:①分别在给出的相似三角形△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
【答案】①见解析;②见解析
【解析】
①按照角平分线的作法分别作出一组对应角的平分线即可;
②先根据△ABC∽△DEF得出∠BAC=∠EDF,∠B=∠E,进而可证△ABG∽△DEH,根据相似三角形的性质有![]() ,则结论可证.
,则结论可证.
解:①如解图所示,AG,DH分别是∠BAC与∠EDF的角平分线;

②已知:如解图,△ABC∽△DEF,![]() =
=![]() =
=![]() =k,AG,DH分别是∠BAC与∠EDF的角平分线.
=k,AG,DH分别是∠BAC与∠EDF的角平分线.
求证:![]() =k.
=k.
证明:∵AG,DH分别是∠BAC与∠EDF的角平分线,
∴∠BAG=![]() ∠BAC,∠EDH=
∠BAC,∠EDH=![]() ∠EDF.
∠EDF.
∵△ABC∽△DEF,
∴∠BAC=∠EDF,∠B=∠E.
∴∠BAG=∠EDH.
∴△ABG∽△DEH.
∴![]() =
=![]() =k.
=k.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目