题目内容
【题目】在平面直角坐标系中,O是坐标原点,抛物线y=﹣x2﹣2x+4交y轴于点B,过点B作AB∥x轴交抛物线于点A,连接OA.将该抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),则m的取值范围是( )
A. 1<m<5 B. 1<m<4 C. 1<m<3 D. 1<m<2
【答案】C
【解析】
设原抛物线的顶点为D,过点D作DE⊥AB于点E交AO于点F.先根据抛物线的解析式求出点B的坐标,再利用对称性求出点A的坐标,再利用二次函数的顶点坐标,根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围.
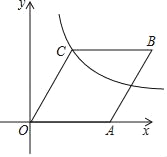
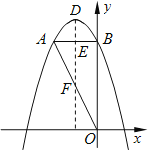
解:如图,设原抛物线的顶点为D,过点D作DE⊥AB于点E交AO于点F.
∵y=﹣x2﹣2x+4=﹣(x+1)2+5,
∴B(0,4),D(﹣1,5),对称轴为直线x=﹣1,
∵AB∥x轴交抛物线于点A,
∴A的坐标(﹣2,4),
∴AB的中点E的坐标是(﹣1,4),
∵OA的中点是F,
∴F的坐标是(﹣1,2),
当D点平移到E点时,平移后得到的抛物线顶点不在△OAB的内部,再继续往下平移正好进入△OAB的内部,
当D点平移到F点时,平移后得到的抛物线顶点正好不在△OAB的内部,
∴m的取值范围是:1<m<3.
故选:C.

练习册系列答案
相关题目