题目内容
【题目】如图,在![]() 中,
中,![]()
![]()
![]() ,垂足为
,垂足为![]() ,过
,过![]() 的⊙O分别与
的⊙O分别与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)当![]() 与⊙O相切时,求⊙O的面积.
与⊙O相切时,求⊙O的面积.
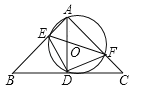
【答案】(1)见解析;(2)![]() .
.
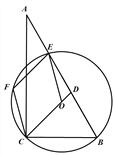
【解析】分析:(1)由等腰直角三角形的性质知AD=CD、∠1=∠C=45°,由∠EAF=90°知EF是⊙O的直径,据此知∠2+∠4=∠3+∠4=90°,得∠2=∠3,利用“ASA”证明即可得;
(2)当BC与⊙O相切时,AD是直径,根据∠C=45°、AC=![]() 可得AD=1,利用圆的面积公式可得答案.
可得AD=1,利用圆的面积公式可得答案.
详解:(1)如图,∵AB=AC,∠BAC=90°,∴∠C=45°.
又∵AD⊥BC,AB=AC,∴∠1=![]() ∠BAC=45°,BD=CD,∠ADC=90°.
∠BAC=45°,BD=CD,∠ADC=90°.
又∵∠BAC=90°,BD=CD,∴AD=CD.
又∵∠EAF=90°,∴EF是⊙O的直径,∴∠EDF=90°,∴∠2+∠4=90°.
又∵∠3+∠4=90°,∴∠2=∠3.在△ADE和△CDF中.
∵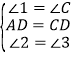 ,∴△ADE≌△CDF(ASA).
,∴△ADE≌△CDF(ASA).
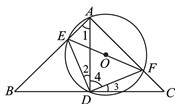
(2)当BC与⊙O相切时,AD是直径.在Rt△ADC中,∠C=45°,AC=![]() ,∴sin∠C=
,∴sin∠C=![]() ,∴AD=ACsin∠C=1,∴⊙O的半径为
,∴AD=ACsin∠C=1,∴⊙O的半径为![]() ,∴⊙O的面积为
,∴⊙O的面积为![]() .
.

练习册系列答案
相关题目
【题目】某校举行“汉字听写”比赛,每名学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.

组别 | 正确字数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
根据以上信息解决下列问题:
(1)在统计表中,![]() ______,
______,![]() ______;
______;
(2)请补全频数分布直方图.
(3)扇形统计图中“C”对应扇形的圆心角的度数是_______.
(4)若该校共有1200名学生参加此次“汉字听写”比赛,估计此次参加比赛听写正确字数不低于24个的学生人数.