题目内容
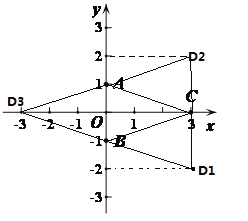
【题目】如图，在平面直角坐标系xOy中，A（0，1），B（0，
），C（3，0）．
（1）若以A、B、C、D为顶点的四边形是平行四边形，则请你写出所有符合条件的D点坐标.
（2）直接写出一个符合（1）中条件的直线AD 的解析式.
（3）求平行四边形ABCD的面积.
【答案】（1）D1(3，-2),D2（3,2），D3（-3,0）（2）y=
x+1（3）6.
【解析】
（1）根据题意在直角坐标系内找到符合的D点坐标即可求解；
（2）可任意选择一点D，再根据A点坐标，利用待定系数法即可求出直线解析式；
（3）根据图像中平行四边形ABCD 即可求解面积.
（1）如图，根据直角坐标系可得D点坐标为D1(3，-2),D2（3,2），D3（-3,0）
（2）设AD2的直线解析式为y=kx+b，
把A（0,1），D2（3,2）代入得
解得
，∴AD2的直线解析式为y=x+1
（3）∵D3（3,0）∴平行四边形ABCD的面积为2×3=6.
【题目】某市公共交通收费如下：
公交票价 | ||
里程（千米） | 票价（元） | 刷卡优惠后付款（元） |
0-10 | 2 | 1 |
10-15 | 3 | 1.5 |
15-20 | 4 | 2 |
20-25 | 5 | 2.5 |
25-30 | 6 | 3 |
以后每增加5千米 | 增加1元 | 增加0.5元 |
地铁票价 | |
里程（千米） | 票价（元） |
0-6 | 3 |
6-12 | 4 |
12-22 | 5 |
22-32 | 6 |
32-52 | 7 |
52-72 | 8 |
以后每增加20千米 | 增加1元 |
（公交票价10千米（含）内2元，不足10千米按10千米计算，其他里程类同；地铁票价6千米（含）内3元，不足6千米按6千米计算，其他里程类同）
（1）张阿姨周日去看望父母，可是张阿姨忘了带一卡通，请你帮助张阿姨思考两个问题：
①若到父母家无论乘公交车还是地铁距离都是24千米，选择哪种公交交通工具费用较少？
②若只用10元钱乘坐公交或地铁，选择哪种公共交通工具乘坐的里程更远？
（2）张阿姨下周日计划使用一卡通刷卡乘公共交通到景点游玩，若里程大于35千米且小于120千米，公交、地铁均可直达.请问：选择公交还是选择地铁出行更省钱？为什么？
