题目内容
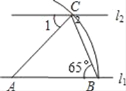
【题目】如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1和l2于B、C两点,连接AC、BC,若∠ABC=65°,则∠1的度数是( )

A. 35° B. 50° C. 65° D. 70°
【答案】B
【解析】
首先由题意可得:AB=AC,根据等边对等角的性质,即可求得∠ACB的度数,又由直线l1∥l2,根据两直线平行,内错角相等,即可求得∠2的度数,然后根据平角的定义,即可求得∠1的度数.
解:根据题意得:AB=AC,
∴∠ACB=∠ABC=67°,
∵直线l1∥l2,
∴∠2=∠ABC=65°,
∵∠1+∠ACB+∠2=180°,
∴∠1=180°﹣∠2﹣∠ACB=180°﹣65°﹣65°=50°.
故选B.

练习册系列答案
相关题目
【题目】某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
A | B | |
载客量(人/辆) | 40 | 20 |
租金(元/辆) | 200 | 150 |
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?