题目内容
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(b,-2a).且![]() +|b-l|=0.CD∥AB,AD∥BC
+|b-l|=0.CD∥AB,AD∥BC
(1)直接写出B、C、D各点的坐标:B 、C 、D ;
(2)如图1,P(3,10),点E,M在四边形ABCD的边上,且E在第二象限.若△PEM是以PE为直角边的等腰直角三角形,请直接写出点E的坐标,并对其中一种情况计算说明;
(3)如图2,F为y轴正半轴上一动点,过F的直线j∥x轴,BH平分∠FBA交直线j于点H.G为BF上的点,且∠HGF=∠FAB,F在运动中FG的长度是否发生变化?若变化,求出变化范围;若不变,求出定值.

【答案】(1)(1,0),(1,8),(-4,8);(2)点E坐标(-1,8)或(-4,7);(3)不发生变化.
【解析】
(1)根据题意可求a=-4,b=1,可得A,B,C三点坐标,由题意可证四边形ABCD是矩形,可求CD=AB=5,AD=BC=8,即可求点D坐标;
(2)分点E在CD上,点EAD上讨论,通过等腰直角三角形的性质和全等三角形的性质,可求点E坐标;
(3)点H作HR⊥BF于点R,通过证△HFR≌△FBO和△HRG≌△FOA,可得RF=1,RG=4,即可求FG=3,则点F在运动中FG的长度不发生变化.
(1)∵![]() +|b-l|=0,
+|b-l|=0,
∴b=1,a=-4,
∴A(-4,0),B(1,0),C(1,8),
∴BC⊥AB,AB=5,BC=8,
∵CD∥AB,AD∥BC,
∴四边形ABCD是平行四边形,且BC⊥AB
∴四边形ABCD是矩形,
∴AD=BC=8,CD=AB=5
∴D(-4,8)
(2)如图,若点E在CD上时,过点E作EN∥y轴,过点M作MN⊥EN于N,过点P作PH⊥EN于点H,
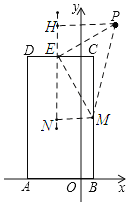
∵∠PEH+∠HPE=90°,∠PEH+∠MEN=90°,
∴∠MEN=∠HPE,且PE=EM,∠PHE=∠MNE=90°,
∴△PHE≌△ENM(AAS)
∴PH=EN,HE=MN=2,
∵CE⊥EN,MN⊥EN,∠DCB=90°,
∴四边形MNEC是矩形,
∴CE=MN=2,且点C(1,8)
∴点E坐标(-1,8)
如图,若点E在AD上,过点P作PH⊥AD,交AD的延长线于H,
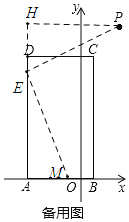
∵∠PEH+∠AEM=90°,∠PEH+∠HPE=90°
∴∠HPE=∠AEM,且PE=EM,∠PHE=∠EAM=90°
∴△PHE≌△EAM(AAS)
∴AE=PH=7
∴点E坐标(-4,7)
(3)不发生变化,
如图,过点H作HR⊥BF于点R,
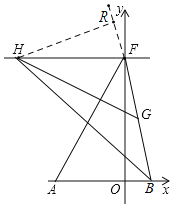
∵BH平分∠ABF,
∴∠FBH=∠ABH,
∵FH∥AB,
∴∠FHB=∠ABH,∠HFR=∠ABF,
∴∠FHB=∠FBH,
∴HF=FB,且∠HFR=∠ABF,∠FOB=∠HRF,
∴△HFR≌△FBO(AAS)
∴RF=OB=1,HR=FO,
∵∠HGF=∠FAB,HR=FO,∠HRG=∠AOF=90°,
∴△HRG≌△FOA(AAS),
∴RG=AO=4,
∴FG=RG-RF=4-1=3,
∴点F在运动中FG的长度不发生变化.





