题目内容
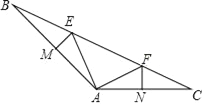
【题目】如图,已知△ABC中∠BAC=135°,点E,点F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,BE=12,CF=9.
(1)判断△EAF的形状,并说明理由;
(2)求△EAF的周长.
【答案】(1)△EAF为直角三角形.理由见解析;(2)△EAF的周长=36.
【解析】
(1)根据线段垂直平分线的性质得出BE=AE,AF=CF,再由∠BAC=135°得出∠B+∠C=180°﹣∠BAC=180°﹣135°=45°,故∠BAE+∠CAF=45°,∠EAF=135°﹣45°=90°由此可得出结论;
(2)由(1)知△EAF是直角三角形,再根据勾股定理求出EF的长,进而可得出结论.
(1)△EAF为直角三角形.
∵EM是AB的垂直平分线,
∴BE=AE,
∴∠BAE=∠B.
∵FN是AC的垂直平分线,
∴AF=CF,
∴∠CAF=∠C
.∵∠BAC=135°,
∴∠B+∠C=180°﹣∠BAC=180°﹣135°=45°,
∴∠BAE+∠CAF=45°,
∴∠EAF=135°﹣45°=90°,
∴△EAF为直角三角形;
(2)在△EAF中,
∵∠EAF=90°,
∴EF2=AE2+AF2,
∵BE=12,CF=9,
∴EF2=122+92=225,
∴EF=15,
∴△EAF的周长=12+9+15=36.
故答案为:(1)△EAF为直角三角形.理由见解析;(2)△EAF的周长=36.

练习册系列答案
相关题目