Question

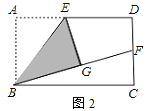
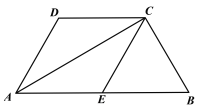
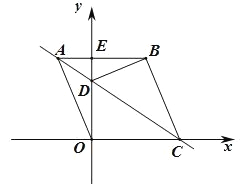
【题目】如图，四边形 ABCO 是菱形，以点 O 为坐标原点，OC 所在直线为轴建立平面直角坐标系.若点 A 的坐 标为(-5，12)，直线 AC、边 AB 与轴的交点分别是点 D 与点 E，连接 BD.

(1)求菱形 ABCO 的边长；

(2)求 BD 所在直线的解析式；

(3)直线 AC 上是否存在一点 P 使得与的面积相等?若存在，请直接写出点 P 的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）菱形 ABCO 的边长为 13；（2） BD 所在直线为；（3）存在点 P 使得△PBD 与△EBD 的面积相等， 点 P 的坐标为或．

【解析】

（1）在Rt△AOE中利用勾股定理即可求得菱形的边长；

（2）根据（1）即可求的OC的长，则C的坐标即可求得，利用待定系数法即可求得直线AC的解析式，求出点D的坐标，再利用待定系数法求BD的解析式即可；

（3）设点P（a, ），根据S△PBD ==S△EBD列式计算即可.

(1)∵四边形 ABCO 为菱形，

∴AB∥CO，

∴∠AEO=∠EOC=90°，

∴在 Rt△EHD 中，

，

∴菱形 ABCO 的边长为 13；

（2）∵四边形 ABCO 为菱形

∴OC=OA=AB=13，

∴BE=AB-AE=13-5=8，

∴点 B 坐标为（8，12），点 C 的坐标为（13，0）， 设 AC 所在直线为 y=kx+b，

根据题意得，

解得，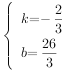

，

∴AC 所在直线为，

∴当 x=0 时，

∴点 D 的坐标为，

同上理可得 BD 所在直线为；

（3）存在点 P 使得△PBD 与△EBD 的面积相等， 点 P 的坐标为或．