题目内容
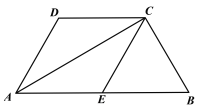
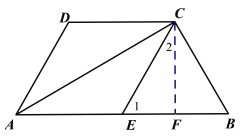
【题目】已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.
(1)求证:四边形AECD是菱形.
(2)若∠DAE=60°,AE=2,求菱形AECD的面积.
【答案】(1)见解析;(2)![]()
【解析】(1)先证AE=CD,AE∥CD,得四边形AECD是平行四边形,再证CE=AE ,得
平行四边形AECD是菱形;
(2)过点C作CF⊥EB交EB于点F. 先求EF,再根据勾股定理求CF,再根据平行四边形面积公式可求出四边形面积.
(1)∵E为AB的中点
∴AB=2AE
∵AB=2CD
∴AE=CD
又∵AB∥CD
∴AE∥CD
∴四边形AECD是平行四边形
∵AC⊥BC
∴∠ACB=90°
又∵E为AB的中点
∴![]() ,
,![]()
∴CE=AE
平行四边形AECD是菱形
(2)过点C作CF⊥EB交EB于点F.
∵四边形AECD是菱形
∴AD∥EC,AE=CE
∴∠DAE=∠1
∵∠DAE=60°,AE=2
∴∠1=60°,CE=2
∵CF⊥EB
∴∠CFE=90°
∴∠1+∠2=90°
∴∠2=30°
∴![]()
![]() ,
,![]()
∴![]()

练习册系列答案
相关题目