题目内容
【题目】正方形ABCD中,E是CD边上一点,
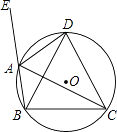
(1)将△ADE绕点A按顺时针方向旋转,使AD,AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 , ∠AFB=∠ 
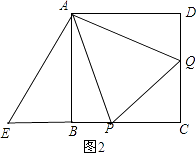
(2)如图2,正方形ABCD中,P,Q分别是BC,CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ 
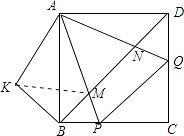
(3)在(2)题中,连接BD分别交AP,AQ于M,N,你还能用旋转的思想说明BM2+DN2=MN2 . 
【答案】
(1)BF;AED
(2)解:将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,
则∠D=∠ABE=90°,
即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,
∵∠PAQ=45°,
∴∠PAE=45°,
∴∠PAQ=∠PAE,
在△APE和△APQ中
∵  ,
,
∴△APE≌△APQ(SAS),
∴PE=PQ,
而PE=PB+BE=PB+DQ,
∴DQ+BP=PQ
(3)解:∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°,
如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,
则∠ABK=∠ADN=45°,BK=DN,AK=AN,
与(2)一样可证明△AMN≌△AMK,得到MN=MK,
∵∠MBA+∠KBA=45°+45°=90°,
∴△BMK为直角三角形,
∴BK2+BM2=MK2,
∴BM2+DN2=MN2.
【解析】解:(1)∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,
∵DE=BF,∠AFB=∠AED.
故答案为:BF,AED;
(1)直接根据旋转的性质得到DE=BF,∠AFB=∠AED;(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ;(3)根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,由于∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2 , 然后利用等相等代换即可得到BM2+DN2=MN2 .

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案