题目内容
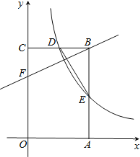
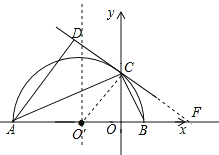
【题目】如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半圆⊙O‘与y轴正半轴交于点C,连接BC,AC.CD是半圆⊙O’的切线,AD⊥CD于点D

(1)求证:∠CAD =∠CAB(3分)
(2)已知抛物线![]() 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=![]() .
.
① 求抛物线的解析式(3分)
② 判断抛物线的顶点E是否在直线CD上,并说明理由(3分);
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由(3分).
【答案】(1)证明见解析;(2)①y=-![]() x2-
x2-![]() x+4;②抛物线顶点E在直线CD上;理由见解析;(3)P1(-10,-6).P2(10,-36).
x+4;②抛物线顶点E在直线CD上;理由见解析;(3)P1(-10,-6).P2(10,-36).
【解析】
试题(1)连接O′C,由CD是⊙O的切线,可得O′C⊥CD,则可证得O′C∥AD,又由O′A=O′C,则可证得∠CAD=∠CAB;
(2)①首先证得△CAO∽△BCO,根据相似三角形的对应边成比例,可得OC2=OAOB,又由tan∠CAO=tan∠CAD=![]() ,则可求得CO,AO,BO的长,然后利用待定系数法即可求得二次函数的解析式;
,则可求得CO,AO,BO的长,然后利用待定系数法即可求得二次函数的解析式;
②首先证得△FO′C∽△FAD,由相似三角形的对应边成比例,即可得到F的坐标,求得直线DC的解析式,然后将抛物线的顶点坐标代入检验即可求得答案;
③根据题意分别从PA∥BC与PB∥AC去分析求解即可求得答案,小心漏解.
试题解析:(1)证明:连接O′C,
∵CD是⊙O′的切线,
∴O′C⊥CD,
∵AD⊥CD,
∴O′C∥AD,
∴∠O′CA=∠CAD,
∵O′A=O′C,
∴∠CAB=∠O′CA,
∴∠CAD=∠CAB;
(2)解:①∵AB是⊙O′的直径,
∴∠ACB=90°,
∵OC⊥AB,
∴∠CAB=∠OCB,
∴△CAO∽△BCO,
∴![]() ,
,
即OC2=OAOB,
∵tan∠CAO=tan∠CAD=![]() ,
,
∴AO=2CO,
又∵AB=10,
∴OC2=2CO(10-2CO),
解得CO1=4,CO2=0(舍去),
∴CO=4,AO=8,BO=2
∵CO>0,
∴CO=4,AO=8,BO=2,
∴A(-8,0),B(2,0),C(0,4),
∵抛物线y=ax2+bx+c过点A,B,C三点,
∴c=4,
由题意得:
![]() ,
,
解得: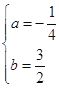 ,
,
∴抛物线的解析式为:y=-![]() x2-
x2-![]() x+4;
x+4;
②设直线DC交x轴于点F,
∴△AOC≌△ADC,
∴AD=AO=8,
∵O′C∥AD,
∴△FO′C∽△FAD,
∴![]() ,
,
∴O′FAD=O′CAF,
∴8(BF+5)=5(BF+10),
∴BF=![]() ,F(
,F(![]() ,0);
,0);
设直线DC的解析式为y=kx+m,
则,
解得: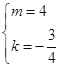 ,
,
∴直线DC的解析式为y=-![]() x+4,
x+4,
由y=-![]() x2-
x2-![]() x+4=-
x+4=-![]() (x+3)2+
(x+3)2+![]() 得顶点E的坐标为(-3,
得顶点E的坐标为(-3,![]() ),
),
将E(-3,![]() )代入直线DC的解析式y=--
)代入直线DC的解析式y=--![]() x+4中,
x+4中,
右边=-![]() ×(-3)+4=
×(-3)+4=![]() =左边,
=左边,
∴抛物线顶点E在直线CD上;
(3)存在,P1(-10,-6),P2(10,-36).
①∵A(-8,0),C(0,4),
∴过A、C两点的直线解析式为y=![]() x+4,
x+4,
设过点B且与直线AC平行的直线解析式为:y=![]() x+b,把B(2,0)代入得b=-1,
x+b,把B(2,0)代入得b=-1,
∴直线PB的解析式为y=![]() x-1,
x-1,
∴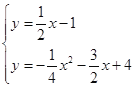 ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴P1(-10,-6).
②求P2的方法应为过点A作与BC平行的直线,
可求出BC解析式,进而求出与之平行的直线的解析式,
与求P1同法,可求出x1=-8,y1=0(舍去);x2=10,y2=-36.
∴P2的坐标(10,-36).
考点: 二次函数综合题.

 阅读快车系列答案
阅读快车系列答案