Question

【题目】如图分别表示步行与骑车在同一路上行驶的路程与时间的关系，根据图象回答下列问题：

（1）出发时与相距 千米；

（2）走了一段路后，自行车发生故障，进行修理，所用的时间是 小时；

（3）出发后 小时与相遇；

（4）求行走的路程与时间的函数关系式．

Answer 1

【答案】（1）10；（2）1；（3）3 ；（4）．

【解析】

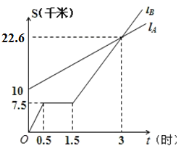
（1）从图上可看出B出发时与A相距10千米．

（2）修理的时间就是路程不变的时间是1.5﹣0.5=1小时．

（3）从图象看出3小时时，两个图象相交，所以3小时时相遇．

（4）S和t的函数关系是一次函数，设函数是为S=kt+b，过（0，10）和（3，22．6），从而可求出关系式．

解：（1）由图形可得B出发时与A相距10千米；

故答案为:1

（2）在图中发现0.5至1.5小时，自行车没有行走，

故可得出修理所用的时间为1小时．

故答案为:1

（3）图中两直线的交点是B与A相遇的时刻，

即出发3小时后与A相遇．

故答案为:3

（4）设函数是为S=kt+b，且过（0，10）和（3，22.6），

则

解得：

故S与时间t的函数关系式为： ．