Question

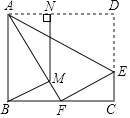
【题目】如图，在矩形ABCD中，AB=3，点E为边CD上一点，将△ADE沿AE所在直线翻折，得到△AFE，点F恰好是BC的中点，M为AF上一动点，作MN⊥AD于N，则BM+AN的最小值为____．

Answer 1

【答案】．

【解析】

根据矩形的性质得到∠BAD=∠ABC=90°，BC=AD，由折叠的性质得到AF=AD，∠FAE=∠DAE，求得∠BAF=30°，∠DAF=60°，得到∠BAF=∠FAE，过B作BG⊥AF交AE于G，则点B与点G关于AF对称，过G作GH⊥AB于H交AF于M，则此时，BM+MH的值最小，推出△ABG是等边三角形，得到AG=BG=AB=5，根据勾股定理即可得到结论．

解：∵四边形ABCD是矩形，

∴∠BAD=∠ABC=90°，BC=AD．

∵将△ADE沿AE所在直线翻折，得到△AFE，

∴AF=AD，∠FAE=∠DAE．

∵点F恰好是BC的中点，

∴BF，

∴∠BAF=30°，

∴∠DAF=60°，

∴∠FAE，

∴∠BAF=∠FAE，

过B作BG⊥AF交AE于G，则点B与点G关于AF对称，

过G作GH⊥AB于H交AF于M，

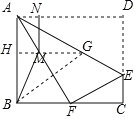
则此时，BM+MH的值最小．

∵MN⊥AD，

∴四边形AHMN是矩形，

∴AN=HM，

∴BM+MH=BM+AN=HG．

∵AB=AG，∠BAG=60°，

∴△ABG是等边三角形，

∴AG=BG=AB=5，

∴，

∴HG，

∴BM+AN的最小值为．

故答案为：．