题目内容
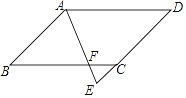
【题目】如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.
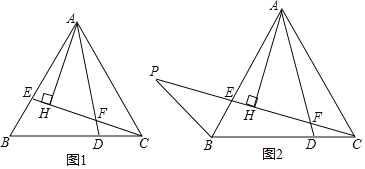
(1)求∠AFE的度数;
(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;
(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=![]() CP,求
CP,求![]() 的值.
的值.
(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)
【答案】(1)∠AFE=60°;(2)见解析;(3)![]()
【解析】
(1)通过证明![]() 得到对应角相等,等量代换推导出
得到对应角相等,等量代换推导出![]() ;
;
(2)由(1)得到![]() ,
,![]() 则在
则在![]() 中利用30°所对的直角边等于斜边的一半,等量代换可得;
中利用30°所对的直角边等于斜边的一半,等量代换可得;
(3)通过在PF上取一点K使得KF=AF,作辅助线证明![]() 和
和![]() 全等,利用对应边相等,等量代换得到比值.(通过将
全等,利用对应边相等,等量代换得到比值.(通过将![]() 顺时针旋转60°也是一种思路.)
顺时针旋转60°也是一种思路.)
(1)解:如图1中.

∵![]() 为等边三角形,
为等边三角形,
∴AC=BC,∠BAC=∠ABC=∠ACB=60°,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() (SAS),
(SAS),
∴∠BCE=∠DAC,
∵∠BCE+∠ACE=60°,
∴∠DAC+∠ACE=60°,
∴∠AFE=60°.
(2)证明:如图1中,∵AH⊥EC,
∴∠AHF=90°,
在Rt△AFH中,∵∠AFH=60°,
∴∠FAH=30°,
∴AF=2FH,
∵![]() ,
,
∴EC=AD,
∵AD=AF+DF=2FH+DF,
∴2FH+DF=EC.
(3)解:在PF上取一点K使得KF=AF,连接AK、BK,
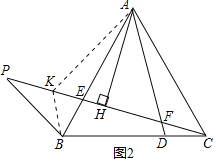
∵∠AFK=60°,AF=KF,
∴△AFK为等边三角形,
∴∠KAF=60°,
∴∠KAB=∠FAC,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() (SAS),
(SAS),![]()
∴∠AKB=∠AFC=120°,
∴∠BKE=120°﹣60°=60°,
∵∠BPC=30°,
∴∠PBK=30°,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴ .
.

练习册系列答案
相关题目