题目内容
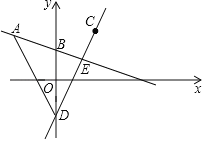
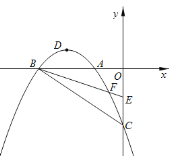
【题目】如图,在平面直角坐标系中,已知抛物线![]() (a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣
(a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣![]() ),该抛物线与BE交于另一点F,连接BC.
),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为![]() 的形式;
的形式;
(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当t=
;(2)当t= ![]() 或
或![]() 时,△OMB为等腰三角形;(3)存在点P,使∠PBF被BA平分,P(
时,△OMB为等腰三角形;(3)存在点P,使∠PBF被BA平分,P(![]() ,
,![]() ).
).
【解析】
(1)根据待定系数法设抛物线解析式为![]() ,代入点C(0,﹣3),即可得出抛物线解析式;(2)抛物线解析式可得顶点D坐标为(-2,1),设M(-2,m),m>1,则MD=
,代入点C(0,﹣3),即可得出抛物线解析式;(2)抛物线解析式可得顶点D坐标为(-2,1),设M(-2,m),m>1,则MD=![]() ,若BM=OM,根据勾股定理得m2+4=m2+1,若BM=OB,则m2+1=9,
,若BM=OM,根据勾股定理得m2+4=m2+1,若BM=OB,则m2+1=9,
若OM=OB,则m2+4=9,根据MD=t×1,逐项计算即可得出t的值;(3)在y轴上取一点N(0,![]() ),连接BN交抛物线于点P则∠PBO=∠EBO,设直线BN的解析式为,
),连接BN交抛物线于点P则∠PBO=∠EBO,设直线BN的解析式为,![]() ,代入点N(0,
,代入点N(0,![]() ),点B(﹣3,0),得直线BN的解析式为
),点B(﹣3,0),得直线BN的解析式为![]() ,与抛物线解析式联立,即可得出结论.
,与抛物线解析式联立,即可得出结论.
解:(1)由题意可设抛物线解析式为![]() ,
,
∵点C(0,﹣3)在抛物线上,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为![]() ;
;
(2)由(1)有![]() ,
,
∴D点坐标为(-2,1),抛物线的对称轴为直线x=-2,
设M(-2,m),m>1,则MD=![]() ,
,
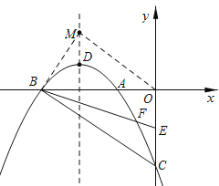
∴OM2=m2+4,BM2=m2+1,
若BM=OM,则m2+4=m2+1,此方程无解,
若BM=OB,则m2+1=9,
解得![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
∴t=MD=![]() ,
,
若OM=OB,则m2+4=9,
解得![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
∴t=MD=![]() ,
,
综上所述,当t=![]() 或
或![]() 时,△OMB为等腰三角形;
时,△OMB为等腰三角形;
(3)存在点P,使∠PBF被BA平分,
在y轴上取一点N(0,![]() ),连接BN交抛物线于点P则∠PBO=∠EBO,
),连接BN交抛物线于点P则∠PBO=∠EBO,
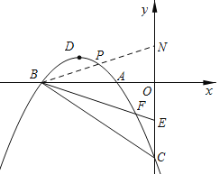
设直线BN的解析式为,![]() ,
,
∴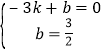 ,解得
,解得![]() ,
,
∴直线BN的解析式为![]() ,
,
解方程组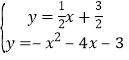 ,得
,得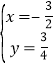 或
或![]() (不合题意,舍去),
(不合题意,舍去),
∴P(![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2