Question

【题目】如图，直线的解析式为，它与坐标轴分别交于A，B两点.

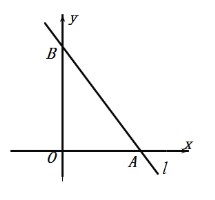
（1）求出点A的坐标；

（2）动点C从y轴上的点出发，以每秒1个单位长度的速度向y轴负半轴运动，求出点C运动的时间t，使得为等腰三角形.

Answer 1

【答案】（1）；（2）当点C运动的时间t是3秒或13秒或秒或16秒时，为等腰三角形.

【解析】

（1）将y=0代入解析式中即可求出结论；

（2）根据等腰三角形腰的情况分类讨论，然后分别画出图形，利用时间=路程÷速度分别求出对应时间即可．

解：（1）令，则，

解得．

则点A的坐标为．

（2）令，则，

则点B的坐标为．

①当时，

若点C在点B上方时，如下图所示：

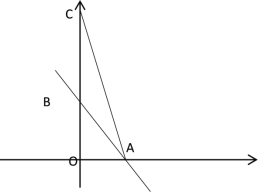
（秒），

若点C在点B上方时，如下图所示：

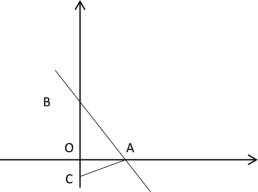
（秒）；

②当时，如下图所示

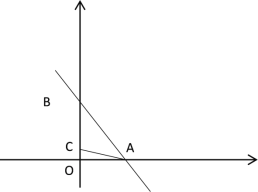
设，

则，

在中，

，

解得

（秒）；

③当时，

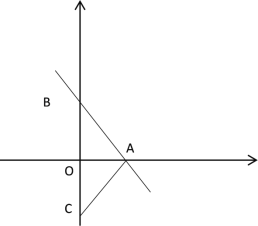
∵AO⊥BC

∴OB=OC=4

（秒）．

综上所述：当点C运动的时间t是3秒或13秒或秒或16秒时，为等腰三角形．