题目内容
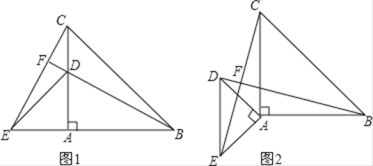
【题目】如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，AF、AG与边BC的交点分别为D、E (点D不与点B重合,点E不与点C重合).
(1)图中共有 对相似而不全等的三角形.
(2)选取其中一对进行证明.
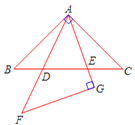
【答案】（1）3；（2）△DAE∽△DCA；
【解析】
（1）观察图形判断哪两个三角形可能相似，再根据所学知识进一步判断；（2）根据“如果两个三角形有两个角对应相等，那么这两个三角形是相似三角形”进行判断.
图中相似而不全等的三角形有：△ABE∽△DAE，△ABE∽△DCA，△DAE∽△DCA.因此答案为3.
∵△ABC和△AFG是等腰直角三角形，
∴∠GAF＝∠ACB，
又∵△DAE和△DCA有一个公共角∠ADE，
∴△DAE∽△DCA.
练习册系列答案
相关题目
