题目内容
【题目】将函数![]() 的图象位于
的图象位于![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折至其上方后,所得的是新函数
轴翻折至其上方后,所得的是新函数![]() 的图象.若该新函数图象与直线
的图象.若该新函数图象与直线![]() 有两个交点,则
有两个交点,则![]() 的取值范围为___________.
的取值范围为___________.
【答案】![]() 或
或![]()
【解析】
根据题意画出新函数的图像,当直线![]() 与
与![]() (
(![]() )只有一个交点时,可得方程
)只有一个交点时,可得方程![]() 有两个相等的实数根,进而可求得此时b的值,将此时的直线向上平移即可得到符合题意的直线;再将点(1,0)和点(
有两个相等的实数根,进而可求得此时b的值,将此时的直线向上平移即可得到符合题意的直线;再将点(1,0)和点(![]() ,0)分别代入直线函数关系式,可得到两个特殊的b的值,结合函数图像可得符合题意的b的取值范围即可.
,0)分别代入直线函数关系式,可得到两个特殊的b的值,结合函数图像可得符合题意的b的取值范围即可.
解:![]() 的图象如图所示:
的图象如图所示:
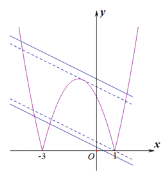
当直线![]() 与
与![]() (
(![]() )
)
只有一个交点时,
函数![]() 的图象与直线
的图象与直线![]() 有三个交点,
有三个交点,
当直线![]() 与
与![]() (
(![]() )只有一个交点,
)只有一个交点,
此时方程![]() 有两个相等的实数根,
有两个相等的实数根,
整理得![]() 有两个相等的实数根,
有两个相等的实数根,
![]() ,
,
解得![]() ,
,
此时直线的解析式为:![]() ,
,
若将此直线向上平移时该新函数图象与直线![]() 有两个交点,此时
有两个交点,此时![]() ;
;
令![]() 中的y=0,
中的y=0,
则![]()
解得:![]()
∴新函数![]() 的图象与x轴的交点坐标为(1,0),(3,0),
的图象与x轴的交点坐标为(1,0),(3,0),
当直线![]() 经过点(1,0)时,
经过点(1,0)时,
函数![]() 的图象与直线
的图象与直线![]() 有三个交点,
有三个交点,
将点(1,0)代入![]()
得:![]() ,
,
![]() ,
,
当直线![]() 经过点(
经过点(![]() ,0)时,
,0)时,
函数![]() 的图象与直线
的图象与直线![]() 有1个交点,
有1个交点,
将点(![]() ,0)代入
,0)代入![]()
得:![]() ,
,
![]() ,
,
∴当该新函数图象与直线![]() 有两个交点时,
有两个交点时,![]() ;
;
综合可知:![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定