题目内容
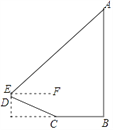
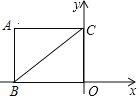
【题目】如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为_____.
【答案】![]() 或
或![]() .
.
【解析】
由题意得出P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,证出PE∥CO,则△PBE∽△CBO,由已知得出点P横坐标为﹣4,OC=6,BO=8,BE=4,由相似对应边成比例得出PE=3即可得出结果;
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,过点P作PE⊥BO于E,证出PE∥CO,则△PBE∽△CBO,由已知得出AC=BO=8,CP=8,AB=OC=6,由勾股定理得出BC=![]() =10,则BP=2,由相似对应边成比例得出PE=
=10,则BP=2,由相似对应边成比例得出PE=![]() ,BE=
,BE=![]() ,则OE=
,则OE=![]() 即可得出结果.
即可得出结果.
解:∵点P在矩形ABOC的内部,且△APC是等腰三角形,
∴P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,如图1所示:
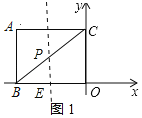
∵PE⊥BO,CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(﹣8,6),
∴点P横坐标为﹣4,OC=6,BO=8,BE=4,
∵△PBE∽△CBO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:PE=3,
∴点P(﹣4,3);
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,
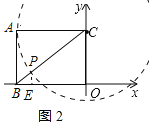
过点P作PE⊥BO于E,如图2所示:
∵CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(﹣8,6),
∴AC=BO=8,CP=8,AB=OC=6,
∴BC=![]() =
=![]() =10,
=10,
∴BP=2,
∵△PBE∽△CBO,
∴![]() =
=![]() =
=![]() ,即:
,即:![]() =
=![]() =
=![]() ,
,
解得:PE=![]() ,BE=
,BE=![]() ,
,
∴OE=8﹣![]() =
=![]() ,
,
∴点P(﹣![]() ,
,![]() );
);
综上所述:点P的坐标为:(﹣![]() ,
,![]() )或(﹣4,3);
)或(﹣4,3);
故答案为(﹣![]() ,
,![]() )或(﹣4,3).
)或(﹣4,3).

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案