题目内容
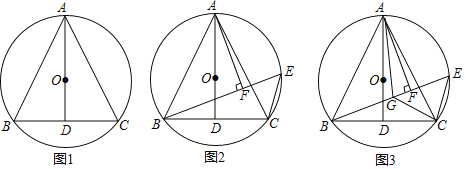
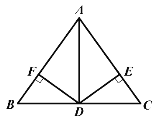
【题目】如图1,边长为4的正方形ABCD中,点E在AB边上(不与点A,B重合),点F在BC边上(不与点B、C重合).
第一次操作:将线段EF绕点F顺时针旋转,当点E落在正方形上时,记为点G;
第二次操作:将线段FG绕点G顺时针旋转,当点F落在正方形上时,记为点H;
依此操作下去…
(1)图2中的△EFD是经过两次操作后得到的,其形状为 ,求此时线段EF的长;
(2)若经过三次操作可得到四边形EFGH.
①请判断四边形EFGH的形状为 ,此时AE与BF的数量关系是 ;
②以①中的结论为前提,设AE的长为x,四边形EFGH的面积为y,求y与x的函数关系式及面积y的取值范围.
【答案】(1)等边三角形,EF=![]() ;(2)①正方形,AE=BF,②y=2x2﹣8x+16(0<x<4),y的取值范围为:8≤y<16.
;(2)①正方形,AE=BF,②y=2x2﹣8x+16(0<x<4),y的取值范围为:8≤y<16.
【解析】
(1)由旋转性质,易得![]() 是等边三角形;利用等边三角形的性质、勾股定理求出EF的长;
是等边三角形;利用等边三角形的性质、勾股定理求出EF的长;
(2)①四边形EFGH是正方形;利用三角形全等证明AE=BF;
②求面积y的表达式,这是一个二次函数,利用二次函数性质求出最值及y的取值范围.
解:(1)如题图2,由旋转性质可知EF=DF=DE,则△DEF为等边三角形.
在Rt△ADE与Rt△CDF中,
![]()
∴Rt△ADE≌Rt△CDF(HL)
∴AE=CF.
设AE=CF=x,则BE=BF=4﹣x
∴△BEF为等腰直角三角形.
∴![]() .
.
∴![]() .
.
在Rt△ADE中,由勾股定理得:AE2+AD2=DE2,即:![]() ,
,
解得:![]() ,
,![]() (舍去)
(舍去)
∴![]() .
.
DEF的形状为等边三角形,EF的长为![]() .
.
(2)①四边形EFGH的形状为正方形,此时AE=BF.理由如下:
依题意画出图形,如答图1所示:连接EG、FH,作HN⊥BC于N,GM⊥AB于M.
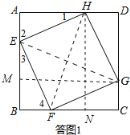
由旋转性质可知,EF=FG=GH=HE,
∴四边形EFGH是菱形,
由△EGM≌△FHN,可知EG=FH,
∴四边形EFGH的形状为正方形.
∴∠HEF=90°
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
∵∠3+∠4=90°,∠2+∠3=90°,
∴∠2=∠4.
在△AEH与△BFE中,
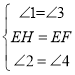
∴△AEH≌△BFE(ASA)
∴AE=BF.
②利用①中结论,易证△AEH、△BFE、△CGF、△DHG均为全等三角形,
∴BF=CG=DH=AE=x,AH=BE=CF=DG=4﹣x.
∴![]() .
.
∴y=2x2﹣8x+16(0<x<4)
∵y=2x2﹣8x+16=2(x﹣2)2+8,
∴当x=2时,y取得最小值8;当x=0时,y=16,
∴y的取值范围为:8≤y<16.
故答案是:(1)等边三角形,![]() ;(2)①正方形,AE=BF,②y=2x2﹣8x+16(0<x<4),y的取值范围为:8≤y<16.
;(2)①正方形,AE=BF,②y=2x2﹣8x+16(0<x<4),y的取值范围为:8≤y<16.

【题目】如图,二次函数![]() 的图象经过坐标原点,与
的图象经过坐标原点,与![]() 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
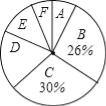
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.