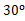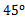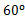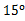题目内容
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△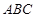 的三个顶点都在格点上.
的三个顶点都在格点上.
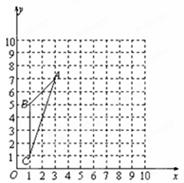
(1)建立如图所示的直角坐标系,请在图中标出△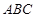 的外接圆的圆心
的外接圆的圆心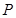 的位置,并填写:
的位置,并填写:
①圆心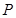 的坐标:
的坐标: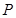 (_______,_______);
(_______,_______);
②⊙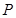 的半径为_______ .
的半径为_______ .
(2)将△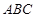 绕点
绕点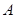 逆时针旋转
逆时针旋转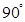 得到△
得到△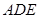 ,画出图形,并求线段
,画出图形,并求线段 扫过的图形的面积.
扫过的图形的面积.
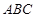 的三个顶点都在格点上.
的三个顶点都在格点上.
(1)建立如图所示的直角坐标系,请在图中标出△
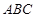 的外接圆的圆心
的外接圆的圆心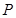 的位置,并填写:
的位置,并填写: ①圆心
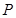 的坐标:
的坐标: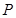 (_______,_______);
(_______,_______);②⊙
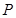 的半径为_______ .
的半径为_______ .(2)将△
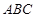 绕点
绕点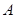 逆时针旋转
逆时针旋转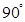 得到△
得到△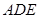 ,画出图形,并求线段
,画出图形,并求线段 扫过的图形的面积.
扫过的图形的面积. (1)(5,3),2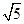 ;(2)8π.
;(2)8π.
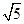 ;(2)8π.
;(2)8π.试题分析:(1)利用外接圆的作法得出P点坐标,进而求出外接圆的半径即可;
(2)根据勾股定理求出AC,根据旋转推出△ABC的面积等于△ADE的面积,根据线段BC扫过的图形的面积=S扇形ACE+S△ABC﹣S扇形ABD﹣S△ADE,根据扇形和三角形的面积公式代入求出即可.
试题解析:(1)如图所示:

①圆心P的坐标:P(5,3);
②⊙P的半径为:
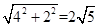 ,
,故答案为:(5,3),2
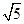 ;
;(2)∵由勾股定理得:AC=2
 ,AB=2
,AB=2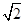 ,
,∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴线段BC扫过的图形的面积=S扇形ACE+S△ABC﹣S扇形ABD﹣S△ADE
=
 =8π.
=8π.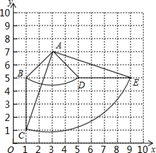 .
.
练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
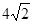 cm,一只蚂蚁由A点出发绕侧面一周后回到A点处,则它爬行的最短路程为________.
cm,一只蚂蚁由A点出发绕侧面一周后回到A点处,则它爬行的最短路程为________.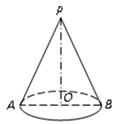
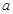 ,面积为
,面积为 ,那么
,那么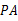 、
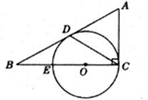
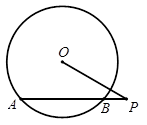
、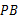 是⊙O的两条切线,
是⊙O的两条切线, 是切点,
是切点,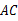 是⊙
是⊙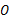 的直径,若∠
的直径,若∠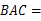 40°,求∠
40°,求∠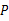 的度数.
的度数.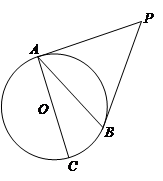
 与BC为直径的半圆
与BC为直径的半圆 相切于点D.
相切于点D.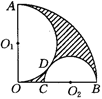
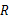 ,⊙
,⊙ ,求
,求 中,直径
中,直径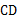 垂直弦
垂直弦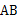 于点
于点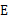 ,连接
,连接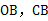 ,已知⊙
,已知⊙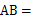
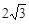 ,则∠
,则∠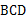 的大小为( )
的大小为( )