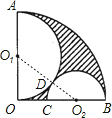
题目内容
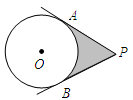
如图,已知扇形AOB,OA⊥OB,C为OB上一点,以OA为直径的半圆 与BC为直径的半圆
与BC为直径的半圆 相切于点D.
相切于点D.
(1)若⊙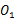 的半径为
的半径为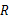 ,⊙
,⊙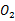 的半径为
的半径为 ,求
,求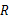 与
与 的比;
的比;
(2)若扇形的半径为12,求图中阴影部分的面积.
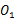 与BC为直径的半圆
与BC为直径的半圆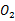 相切于点D.
相切于点D.
(1)若⊙
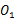 的半径为
的半径为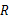 ,⊙
,⊙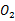 的半径为
的半径为 ,求
,求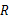 与
与 的比;
的比;(2)若扇形的半径为12,求图中阴影部分的面积.
(1)3:2 (2)10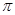
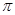
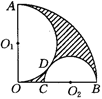
分析:(1)如图,连接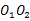 ,则
,则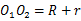 ,在直角三角形
,在直角三角形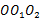 中,由勾股定理可以求出
中,由勾股定理可以求出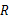 与
与 的关系.
的关系.
(2)扇形的半径为12,即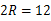 ,
,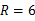 ,根据(1)的结论可以求出
,根据(1)的结论可以求出 ,则阴影部分的面积等于扇形的面积减去两个半圆的面积.
,则阴影部分的面积等于扇形的面积减去两个半圆的面积.
解:(1)连接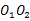 ,则
,则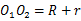 ,
, 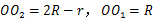 .
.
在Rt△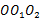 中,由勾股定理,得
中,由勾股定理,得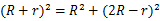 ,
,
整理得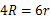 ,∴
,∴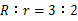 .
.
(2)∵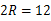 ,∴
,∴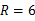 ,∴
,∴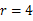 ,
,
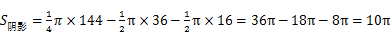 .
.
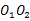 ,则
,则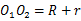 ,在直角三角形
,在直角三角形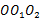 中,由勾股定理可以求出
中,由勾股定理可以求出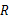 与
与 的关系.
的关系.
(2)扇形的半径为12,即
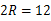 ,
,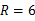 ,根据(1)的结论可以求出
,根据(1)的结论可以求出 ,则阴影部分的面积等于扇形的面积减去两个半圆的面积.
,则阴影部分的面积等于扇形的面积减去两个半圆的面积.解:(1)连接
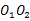 ,则
,则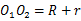 ,
, 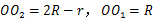 .
.在Rt△
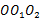 中,由勾股定理,得
中,由勾股定理,得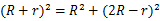 ,
,整理得
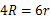 ,∴
,∴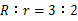 .
.(2)∵
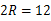 ,∴
,∴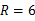 ,∴
,∴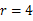 ,
,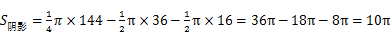 .
.
练习册系列答案
相关题目
 圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为__________.
圆周的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为__________.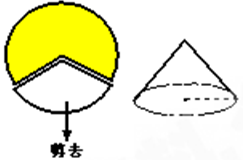
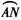 的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .
的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .
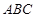 的三个顶点都在格点上.
的三个顶点都在格点上.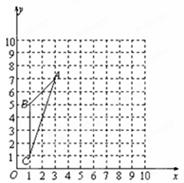
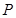 的位置,并填写:
的位置,并填写: 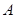 逆时针旋转
逆时针旋转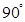 得到△
得到△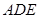 ,画出图形,并求线段
,画出图形,并求线段 扫过的图形的面积.
扫过的图形的面积. 
 ,直线AB为⊙O的切线,B为切点.则B点的坐标为__________.
,直线AB为⊙O的切线,B为切点.则B点的坐标为__________.
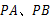 切⊙O于
切⊙O于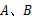 两点,若
两点,若 ⊙O的半径为
⊙O的半径为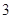 ,则阴影部分的面积为_______.
,则阴影部分的面积为_______.