Question

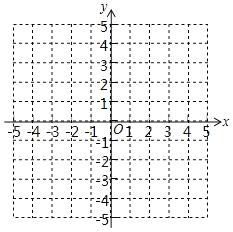
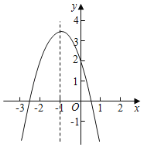
【题目】二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝﹣1，有以下结论：①abc＜0；②2a﹣b＝0；③4ac﹣b2＜8a；④3a+c＜0；⑤a﹣b＜m（am+b），其中正确的结论的个数是（　　）

A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

①根据抛物线的开口方向、对称轴、与轴的交点即可得结论；

②根据抛物线的对称轴即可得结论；

③根据抛物线与轴的交点个数即可得结论；

④根据抛物线的对称轴和等于1时小于0即可得结论；

⑤根据抛物线的顶点坐标及其它任何坐标的纵坐标进行比较即可得结论．

解：①根据抛物线可知：

，，，，

所以①错误；

②因为对称轴，即，

，．

所以②正确；

③因为抛物线与轴有两个交点，

所以，

所以．

所以③正确；

④当时，，

即，

所以，

所以．

所以④正确；

⑤当时，有最大值，

所以当时，的值最大，

当时，，

所以，

即．

所以⑤错误．

所以有②③④正确．

故选C．