题目内容
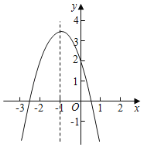
【题目】已知二次函数的解析式是y＝﹣x2+2x+3．
（1）用配方法将该二次函数化成y＝a（x﹣h）2+k的形式，并写出顶点坐标；
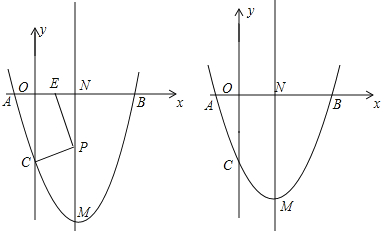
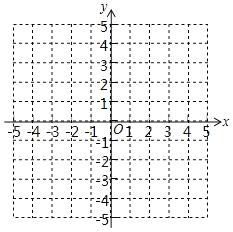
（2）在图中画出该二次函数的图象（不需要列表），并写出该图象与x轴的交点；
（3）当0≤x＜3时，直接写出y的取值范围．
【答案】（1）y＝﹣（x﹣1）2+4，顶点坐标为（1，4）；（2）图详见解析，（﹣1，0），（3，0）；（3）0＜y≤4．
【解析】
（1）利用配方法得到y＝﹣（x﹣1）2+4，则根据二次函数的性质得到抛物线的顶点坐标；
（2）解方程﹣x2+2x+3＝0得抛物线与x轴的交点坐标，然后描点画出二次函数的图象；
（3）结合函数图象和二次函数的性质写出y的取值范围．
解：（1）y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
所以抛物线的顶点坐标为（1，4）；
（2）当y＝0时，﹣x2+2x+3＝0，解得x1＝﹣1，x2＝3，抛物线与x轴的交点坐标为（﹣1，0），（3，0），
如图，
（3）当0≤x＜3时，y的取值范围为0＜y≤4．
练习册系列答案
状元坊全程突破导练测系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
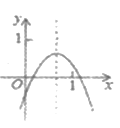
【题目】函数y＝x2+3x+2的图象如图1所示，根据图象回答问题：
（1）当x满足 时，x2+3x+2＞0；
（2）在解决上述问题的基础上，探究解决新问题：
①函数y＝
的自变量x的取值范围是 ；
②下表是函数y＝的几组y与x的对应值．
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477 … | 4.472 … | 2.449 … | 1.414 … | 0 | 0 | 1.414 … | 2.449 … | 4.472 … | 5.477 … | … |
如图2，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点的大概位置，请你根据描出的点，画出该函数的图象：
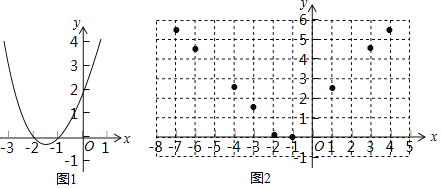
③利用图象，直接写出关于x的方程x4=x2+3x+2的所有近似实数解 （结果精确到0.1）
