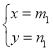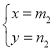题目内容
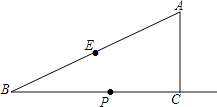
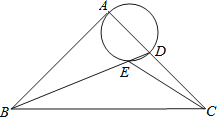
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为___.
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为___.
【答案】![]() ﹣2
﹣2
【解析】
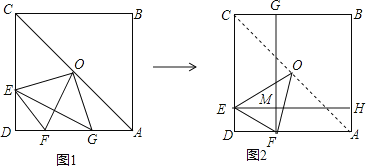
连结AE,如图1,先根据等腰直角三角形的性质得到AB=AC=4,再根据圆周角定理,由AD为直径得到∠AED=90°,接着由∠AEB=90°得到点E在以AB为直径的 O上,于是当点O、E、C共线时,CE最小,如图2,在Rt△AOC中利用勾股定理计算出OC=2![]() ,从而得到CE的最小值为2
,从而得到CE的最小值为2![]() ﹣2.
﹣2.
连结AE,如图1,
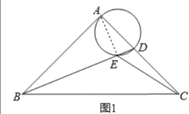
∵∠BAC=90°,AB=AC,BC=![]() ,
,
∴AB=AC=4,
∵AD为直径,
∴∠AED=90°,
∴∠AEB=90°,
∴点E在以AB为直径的O上,
∵O的半径为2,
∴当点O、E. C共线时,CE最小,如图2
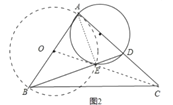
在Rt△AOC中,∵OA=2,AC=4,
∴OC=![]() ,
,
∴CE=OCOE=2![]() ﹣2,
﹣2,
即线段CE长度的最小值为2![]() ﹣2.
﹣2.
故答案为:2![]() ﹣2.
﹣2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据:
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题:
(1)请直接写出表格中![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由;
(3)为了让学生重视安全知识的学习,学校将给竞赛成绩满分的同学颁发奖状,该校七年级新生共570人,试估计需要准备多少张奖状?