题目内容
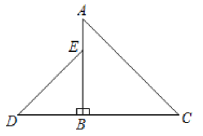
【题目】如图,![]() 、都是等腰直角三角形,
、都是等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() .将
.将![]() 绕点B逆时针方向旋转后得
绕点B逆时针方向旋转后得![]() ,当点
,当点![]() 恰好落在线段
恰好落在线段![]() 上时,则
上时,则![]() ______.
______.
【答案】![]()
【解析】
如图,连接CE′,根据等腰直角三角形的性质得到AB=BC=![]() ,BD=BE=2,根据旋转的性质得到D′B=BE′=BD=2,∠D′BE′=90′,∠D′BD=∠ABE′,由全等三角形的性质得到∠D′=∠CE′B=45°,过B作BH⊥CE′于H,利用勾股定理求出CH即可得到结论.
,BD=BE=2,根据旋转的性质得到D′B=BE′=BD=2,∠D′BE′=90′,∠D′BD=∠ABE′,由全等三角形的性质得到∠D′=∠CE′B=45°,过B作BH⊥CE′于H,利用勾股定理求出CH即可得到结论.
如图,连接CE′,
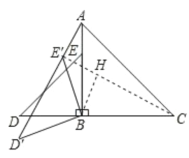
∵△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=![]() ,
,
∴AB=BC=![]() ,BD=BE=2,
,BD=BE=2,
∵将△BDE绕点B逆时针方向旋转后得△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90′,∠D′BD=∠ABE′,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°,
过B作BH⊥CE′于H,
在Rt△BHE′中,BH=E′H=![]() BE′=
BE′=![]()
在Rt△BCH中,CH=![]()
∴CE′=![]()
故答案为:![]() .
.

练习册系列答案
相关题目
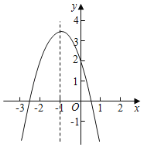
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;

(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).