题目内容
【题目】抛物线F1：y＝ax2+bx﹣1（a＞1）与x轴交于点A、B（点A在点B的左侧），与y轴于点C，已知点A的坐标为（﹣
，0），
（1）直接写出b＝ （用含a的代数式表示）；
（2）求点B的坐标；
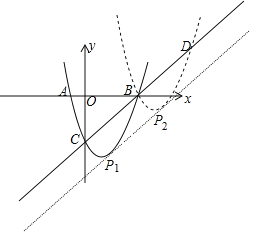
（3）设抛物线F1的顶点为P1，将该抛物线平移后得到抛物线F2，抛物线F2的顶点P2满足P1P2∥BC，并且抛物线F2过点B，
①设抛物线F2与直线BC的另一个交点为D，判断线段BC与CD的数量关系（不需证明），并直接写出点D的坐标；
②求出抛物线F2与y轴的交点纵坐标的取值范围．
【答案】（1）1﹣a；（2）B（1，0）；（3）①CD＝2BC，D（2，1）；②c＞1．
【解析】
（1）将点A（﹣
，0）的坐标代入抛物线表达式并整理得：b＝1﹣a，即可求解；
（2）抛物线的表达式为：y＝ax2+（1﹣a）x﹣1，令y＝0，则x＝1或﹣，故点B（1，0）；
（3）①根据平移的性质可得BC=P1P2＝BD，从而得出CD＝2BC；
②先令x＝0，则y＝-1，从而得出C点坐标，再根据BC＝BD，得出D点坐标，平移后的图象过点B（1，0），点D（2，1），将点B、D的坐标代入抛物线表达式：y＝ax2+b′x+c得：c＝2a-1即可求解．
解：（1）点A的坐标为（﹣，0），
将点A的坐标代入抛物线表达式并整理得：b＝1﹣a，
故答案为：1﹣a；
（2）抛物线的表达式为：y＝ax2+（1﹣a）x﹣1
令y＝0，则x＝1或﹣，
故点B（1，0）；
（3）①根据平移的性质可得BC=P1P2＝BD，所以CD＝2BC；
②对于y＝ax2+bx﹣1，令x＝0，则y=-1；则点C（0，-1）
因为点B是C、D的中点，B点坐标（1，0）由中点公式得：点D（2，1）；
设平移后抛物线表达式为：y＝ax2+b′x+c，图象过点B（1，0），点D（2，1），
将点B、D的坐标代入抛物线表达式：y＝ax2+b′x+c得：
，
解得：c＝2a-1
因为a＞1，所以c＝2a-1＞1
抛物线F2与y轴的交点纵坐标的取值范围为：c＞1．
