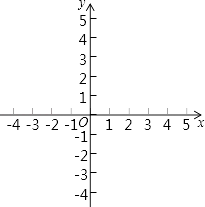Question

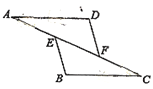
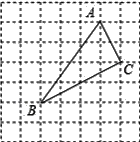
【题目】如图，在7×7网格中，每个小正方形的边长都为1．

（1）建立适当的平面直角坐标系后，若点A（3，4）、C（4，2），则点B的坐标为　　　　　　；

（2）图中格点△ABC的面积为　　　　　　；

（3）判断格点△ABC的形状，并说明理由．

Answer 1

【答案】（1）（0，0）；（2）5 ；（3）直角三角形

【解析】

（1）由已知点的坐标即可得出点B为坐标原点，即可得出结果；

（2）图中格点△ABC的面积=矩形的面积减去3个直角三角形的面积，即可得出结果；

（3）由勾股定理可得：AB2=25，BC2=20，AC2=5，得出BC2+AC2=AB2，由勾股定理的逆定理即可得出结论．

（1）解：∵点A（3，4）、C（4，2），

∴点B的坐标为（0，0）；

故答案为：（0，0）；

（2）解：图中格点△ABC的面积=4×4-1212×4×2-1212×4×3-1212×2×1=5；

故答案为：5；

（3）解：格点△ABC是直角三角形．理由如下：

由勾股定理可得：AB2=32+42=25，BC2=42+22=20，AC2=22+12=5，

∴BC2+AC2=20+5=25，AB2=25，

∴BC2+AC2=AB2，

∴△ABC是直角三角形．