��Ŀ����
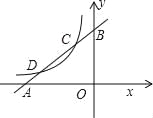
����Ŀ����֪��ͼ������������A��B���㣬����ʾ�����ֱ���n��n+6��A����ÿ��5����λ���ȵ��ٶ������˶���ͬʱ��B��ÿ��3����λ���ȵ��ٶ�Ҳ�����˶������˶�ʱ��Ϊt��.
(1)��n=1ʱ������t��A���ʾ������_______��B���ʾ������______��AB=________��
(2)��tΪ��ֵʱ��A��B�����غϣ�
(3)�������˶��Ĺ����У���PΪ�߶�AB���е㣬�����ϵ�C��ʾ������n+10.�Ƿ����tֵ��ʹ���߶�PC=4�������ڣ���t��ֵ���������ڣ���˵������.
![]()
���𰸡�(1)5t+1��3t+7��![]() ��(2)t=3ʱ��A��B�����غϣ�(3)����t��ֵ��ʹ���߶�PC=4����ʱ
��(2)t=3ʱ��A��B�����غϣ�(3)����t��ֵ��ʹ���߶�PC=4����ʱ![]() ��
��![]() .
.
��������
��1����n=1�����A��B��ʾ�����У�Ȼ���������������Ҽӵ�ԭ��ɱ�ʾ������t��A���ʾ������B���ʾ�������ٸ��������ľ��빫ʽ�������AB�ij��ȣ�
��2�����ݵ�A��B�غϼ��ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��3�����ݵ�A��B��ʾ������ϵ�PΪ�߶�AB���е㼴���ҳ���P��ʾ����������PC=4���ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
(1) �ߵ�n=1ʱ��n+6=1+6=7,
������t��A���ʾ������5t+1��B���ʾ����3t+7��
��AB=(3t+7)-( 5t+1)=![]() ,
,
�ʴ�Ϊ��5t+1��3t+7��![]()
(2)��������ã�![]() ��
��
��t=3ʱ��A��B�����غϣ�
(3)��P���߶�AB���е㣬
���P��ʾ����Ϊ![]() ��
��
��PC=4��
����![]() ��
��
�����t��ֵ��ʹ���߶�PC=4����ʱ![]() .
.