题目内容
【题目】如图,已知反比例函数y1=![]() 的图象与一次函数:y2=ax+b的图象相交于点A(1,4)、B(m,﹣2)
的图象与一次函数:y2=ax+b的图象相交于点A(1,4)、B(m,﹣2)
(1)求出反比例函数和一次函数的关系式;
(2)观察图象,直按写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C是x轴上的点,且△ABC的面积面积为6,求点C的坐标.
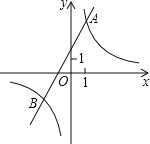
【答案】(1)反比例函数的解析式为y1=![]() ,一次函数的解析式为 y2=2x+2;(2)﹣2<x<0或x>1;(3)C的坐标(1,0)或(﹣3,0).
,一次函数的解析式为 y2=2x+2;(2)﹣2<x<0或x>1;(3)C的坐标(1,0)或(﹣3,0).
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据一次函数图象在上方的部分是不等式的解,可得答案;
(3)根据面积的和差,可得答案.
(1)∵函数y1=![]() 的图象过点A(1,4),即4=
的图象过点A(1,4),即4=![]() ,
,
∴k=4,即y1=![]() ,
,
又∵点B(m,﹣2)在y1=![]() 上,
上,
∴m=﹣2,
∴B(﹣2,﹣2),
又∵一次函数y2=ax+b过A、B两点,
即 ![]() ,
,
解之得![]() .
.
∴y2=2x+2.
反比例函数的解析式为y1=![]() ,
,
一次函数的解析式为 y2=2x+2;
(2)要使y1<y2,即函数y1的图象总在函数y2的图象下方,
∴﹣2<x<0或x>1;
(3)如图,直线AB与x轴交点E的坐标(﹣1,0),
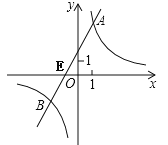
∴S△ABC=S△AEC+S△BEC=![]() EC×4+
EC×4+![]() EC×2=6.
EC×2=6.
∴EC=2,
-1+2=1,-1-2=-3,
∴C的坐标(1,0)或(﹣3,0).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目